2 多元线性回归
1. 简介
多元线性回归是一种统计建模方法,用于研究多个自变量与一个因变量之间的关系。它是简单线性回归的扩展,简单线性回归只涉及一个自变量和一个因变量。在多元线性回归中,我们可以使用多个自变量来预测一个因变量。
多元线性回归的基本原理是通过拟合一个线性模型来描述自变量与因变量之间的关系。这个线性模型通常采用最小二乘法来估计参数,使得模型预测值与实际观测值之间的残差平方和最小化。
多元线性回归模型的一般形式可以表示为:
y = β 0 + β 1 x 1 + β 2 x 2 + . . . + β n x n + ϵ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_n x_n + \epsilon y=β0+β1x1+β2x2+...+βnxn+ϵ
其中, y y y 是因变量, x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn 是自变量, β 0 , β 1 , . . . , β n \beta_0, \beta_1, ..., \beta_n β0,β1,...,βn 是回归系数, ϵ \epsilon ϵ 是误差项。
通过多元线性回归分析,我们可以确定自变量与因变量之间的关系强度和方向,并且可以对因变量进行预测和解释。
2. 例子与底层的手动实现
2.1 目标
假设我们想要预测一个人的体重(因变量)基于他们的身高、年龄和性别(自变量)。我们可以收集一组数据,包括许多人的身高、年龄、性别和相应的体重。
数据可能看起来像这样:
| 身高(cm) | 年龄(岁) | 性别 | 体重(kg) |
|---|---|---|---|
| 170 | 30 | 男 | 75 |
| 160 | 45 | 女 | 65 |
| 180 | 25 | 男 | 85 |
| 165 | 35 | 女 | 70 |
| … | … | … | … |
我们的目标是建立一个多元线性回归模型,以便基于身高、年龄和性别来预测体重。
2.2 选择模型——多元线性模型
假设我们使用以下形式的线性模型:
体重 = β 0 + β 1 × 身高 + β 2 × 年龄 + β 3 × 性别 体重 = \beta_0 + \beta_1 \times 身高 + \beta_2 \times 年龄 + \beta_3 \times 性别 体重=β0+β1×身高+β2×年龄+β3×性别
其中, β 0 , β 1 , β 2 , β 3 \beta_0, \beta_1, \beta_2, \beta_3 β0,β1,β2,β3 是模型的系数(参数),而身高、年龄和性别是自变量。
现在我们的任务就是求解最合适的参数。
2.3 如何求解参数
那么如何选择合适的参数呢?
这就需要指定一个规则:
- 这个规则要满足在参数最好的情况下,规则体现也最好
- 对于参数设置不好的情况,那么规则也对应差
这个规则我们就称之为损失函数。
在多元线性回归模型中,损失函数(或成本函数)是衡量模型预测值与实际观测值之间差异的一个指标。它的目的是量化模型的预测值和实际值之间的误差。常用的损失函数是平方误差损失函数,这是因为它具有良好的数学性质,使得求解过程相对简单,并且在很多情况下能够给出合理的估计结果。
平方误差损失函数
平方误差损失函数定义为所有观测值的预测误差的平方和。如果我们有 n n n 个观测值,模型的预测值表示为 Y ^ \hat{Y} Y^,实际观测值表示为 Y Y Y,那么平方误差损失函数 S S S 可以表示为:
S = ∑ i = 1 n ( y i − y ^ i ) 2 S = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 S=i=1∑n(yi−y^i)2
其中, y i y_i yi 是第 i i i 个观测的实际值, y ^ i \hat{y}_i y^i 是模型对第 i i i 个观测的预测值。其实就是我们上一篇文章讲的损失函数。
现在我们的目的就是找到对应的 β 0 , β 1 , β 2 , β 3 \beta_0, \beta_1, \beta_2, \beta_3 β0,β1,β2,β3,使得最后根据上述公式计算的结果最小。
2.4 为什么需要用矩阵表示?
矩阵表示在多元线性回归和许多其他数据分析、机器学习方法中至关重要,主要由于以下几点原因:
- 计算效率
使用矩阵表示可以充分利用现代计算机和数学软件库(如NumPy、MATLAB)的高效矩阵运算能力,使得对大规模数据集的处理更加快速和高效。矩阵运算可以并行处理,这意味着可以同时计算多个数据点或特征的运算,显著提高计算速度。
- 数学表达的简洁性
矩阵表示使复杂的数学运算和模型变得更加简洁易懂。比如,在多元线性回归中,使用矩阵可以将整个模型的预测和系数估计压缩为几个简洁的数学式子。这种表达方式不仅便于理解和推导,还方便了模型的实现和分析。
- 泛化能力
矩阵表示让模型的推广变得更加容易。无论是增加更多的观测数据,还是引入更多的自变量,模型的核心数学表达形式保持不变,只需调整矩阵的大小即可。这种灵活性使得矩阵表示非常适合处理各种规模和复杂度的问题。
- 理论分析
在理论分析和证明中,矩阵表示为我们提供了一种强大的工具。它允许我们使用线性代数的理论来研究模型的性质,比如可解性、稳定性和最优性等。通过矩阵的特征值、奇异值等,我们可以深入理解模型的行为和性能限制。
- 统一的框架
矩阵表示为不同类型的数据分析和机器学习算法提供了一个统一的框架。许多算法,无论是监督学习还是非监督学习,都可以通过矩阵和向量来表达,这有助于在不同算法之间建立联系,以及将一种算法的洞察应用到另一种算法中。
- 数据结构对应
在实际应用中,数据通常以表格形式存在,其中行代表观测值,列代表特征。矩阵自然地对应于这种数据结构,使得数据的处理、变换和分析更加直接和方便。
核心就主要集中在前三点,所以基于以上原因,我们需要使用矩阵来进行运算。
为了方便后续内容的理解,先看下面一个实例理解一下矩阵:
假设我们有一个多元线性回归问题,其中有一个因变量 Y Y Y(比如房屋价格),和两个自变量 X 1 X_1 X1(比如房屋的面积)和 X 2 X_2 X2(比如房屋的年龄)。我们有3个观测值,现在我们使用矩阵来表示这个多元线性回归模型。
观测数据
观测 Y Y Y (房价) X 1 X_1 X1 (面积) X 2 X_2 X2 (年龄) 1 300 1000 5 2 400 1500 3 3 350 1200 4 矩阵表示
在多元线性回归模型中,我们通常在自变量矩阵 X X X 中添加一列1来代表截距项 β 0 \beta_0 β0。因此,我们的矩阵 X X X 和向量 Y Y Y 可以表示如下:
- Y Y Y = [ 300 400 350 ] \begin{bmatrix} 300 \\ 400 \\ 350 \end{bmatrix} 300400350
-
X
X
X =
[
1
1000
5
1
1500
3
1
1200
4
]
\begin{bmatrix} 1\space \space \space 1000\space \space \space 5 \\ 1\space \space \space 1500\space \space \space 3 \\ 1\space \space \space 1200\space \space \space 4 \end{bmatrix}
1 1000 51 1500 31 1200 4
其中, X X X 矩阵的第一列是全1,代表截距项,第二列是自变量 X 1 X_1 X1 的值,第三列是自变量 X 2 X_2 X2 的值。
之所以第一列设置为截距项:
截距项 β 0 β_0 β0 代表了当所有自变量 X 的值都为0时,因变量 Y 的期望值。在许多实际情况下,即使所有的自变量都是0,因变量也可能不为0。因此,截距项是模型的一个重要组成部分,可以提供更完整的数据拟合。
2.5 关于最小化损失情况下参数求解公式的推导
损失函数的矩阵化表示
在矩阵的形式中,我们可以将损失函数 S S S 表示为:
S = ( Y − X β ) T ( Y − X β ) S = (Y - X\beta)^T(Y - X\beta) S=(Y−Xβ)T(Y−Xβ)
这里,
- Y Y Y 是一个 n × 1 n \times 1 n×1 的列向量,包含了所有的实际观测值。
- X X X 是一个 n × ( p + 1 ) n \times (p+1) n×(p+1) 的设计矩阵,包含了所有的自变量值以及一列全1(对应截距项)。
- β \beta β 是一个 ( p + 1 ) × 1 (p+1) \times 1 (p+1)×1 的列向量,包含了模型的所有系数(包括截距项)。
-
X
β
X\beta
Xβ 表示模型的预测值。
矩阵X的模式:
X = [ 1 X 11 X 12 … X 1 n 1 X 21 X 22 … X 2 n ⋮ ⋮ ⋮ ⋱ ⋮ 1 X m 1 X m 2 … X m n ] X = \begin{bmatrix} 1 \space\space\space X_{11} \space\space\space X_{12} \space\space\space \dots \space\space\space X_{1n} \\ 1 \space\space\space X_{21} \space\space\space X_{22} \space\space\space \dots \space\space\space X_{2n} \\ \vdots \space\space\space \vdots \space\space\space \vdots \space\space\space \ddots \space\space\space \vdots \\ 1 \space\space\space X_{m1} \space\space\space X_{m2} \space\space\space \dots \space\space\space X_{mn} \end{bmatrix} X= 1 X11 X12 … X1n1 X21 X22 … X2n⋮ ⋮ ⋮ ⋱ ⋮1 Xm1 Xm2 … Xmn
矩阵 β \beta β的模式:
β = [ β 0 β 1 β 2 ⋮ β p ] \beta = \begin{bmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \\ \vdots \\ \beta_p \end{bmatrix} β= β0β1β2⋮βp
为了详细说明 X β X\beta Xβ 的运算过程,我们将使用前面的例子中的矩阵 X X X 和系数向量 β \beta β。假
设我们已经通过某种方法(例如最小二乘法)计算出了 β \beta β 的估计值。在我们的例子中, β \beta β 的估计值如下:
β ^ = [ β 0 β 1 β 2 ] = [ 550 0 − 50 ] \hat{\beta} = \begin{bmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \end{bmatrix} = \begin{bmatrix} 550 \\ 0 \\ -50 \end{bmatrix} β^= β0β1β2 = 5500−50
X X X 矩阵(包含截距项的自变量矩阵)如下:
X = [ 1 1000 5 1 1500 3 1 1200 4 ] X = \begin{bmatrix} 1 \space\space\space 1000 \space\space\space 5 \\ 1 \space\space\space 1500 \space\space\space 3 \\ 1 \space\space\space 1200 \space\space\space 4 \end{bmatrix} X= 1 1000 51 1500 31 1200 4
现在,我们将展示如何计算 X β X\beta Xβ:
X β = [ 1 1000 5 1 1500 3 1 1200 4 ] [ 550 0 − 50 ] X\beta = \begin{bmatrix} 1 \space\space\space 1000 \space\space\space 5 \\ 1 \space\space\space 1500 \space\space\space 3 \\ 1 \space\space\space 1200 \space\space\space 4 \end{bmatrix} \begin{bmatrix} 550 \\ 0 \\ -50 \end{bmatrix} Xβ= 1 1000 51 1500 31 1200 4 5500−50
这个乘法操作的结果是一个列向量,每个元素是 X X X 的每一行与 β \beta β 的点积(或者说是内积)。
然后再解释一下,原本我们的损失函数为:
S = ∑ i = 1 n ( y i − y ^ i ) 2 S = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 S=i=1∑n(yi−y^i)2
转换成矩阵表示就是:
S = ( Y − X β ) 2 S = (Y - X\beta)^2 S=(Y−Xβ)2
因为矩阵包含了所有的X与Y,所以没必要求和。但是上式是不一定能运算的,因为矩阵运算有A行B列不能直接×A行B列,要乘B列A行,所以需要转置:
S = ( Y − X β ) T ( Y − X β ) S = (Y - X\beta)^T(Y - X\beta) S=(Y−Xβ)T(Y−Xβ)
转置的运算规则
先讲一下转置运算的常用规则:
这里是一些基本的转置运算规则:
- 基本定义
- 若
A
A
A 是一个
m
×
n
m \times n
m×n 矩阵,那么
A
A
A 的转置,记作
A
′
A'
A′ 或
A
T
A^T
AT,是一个
n
×
m
n \times m
n×m 矩阵,其元素满足:如果
a
i
j
a_{ij}
aij 是
A
A
A 中的元素(第
i
i
i 行,第
j
j
j 列),那么在
A
′
A'
A′ 中的对应元素
a
′
∗
j
i
a'*{ji}
a′∗ji(第
j
j
j 行,第
i
i
i 列)等于
a
∗
i
j
a*{ij}
a∗ij。
- 转置的转置
- 对任意矩阵
A
A
A,
(
A
′
)
′
=
A
(A')' = A
(A′)′=A。这意味着如果你对一个矩阵进行两次转置,你会回到原始矩阵。
- 加法
- 对于任意两个同型矩阵
A
A
A 和
B
B
B,
(
A
+
B
)
′
=
A
′
+
B
′
(A + B)' = A' + B'
(A+B)′=A′+B′。这意味着两个矩阵先加后转置,与先转置再加是等价的。
- 数乘
- 对于任意矩阵
A
A
A 和任意标量
k
k
k,
(
k
A
)
′
=
k
A
′
(kA)' = kA'
(kA)′=kA′。这意味着可以先对矩阵进行标量乘法,然后转置,或者先转置矩阵再进行标量乘法,结果是相同的。
- 矩阵乘法
- 对于两个矩阵
A
A
A 和
B
B
B,其中
A
A
A 的列数等于
B
B
B 的行数,那么
(
A
B
)
′
=
B
′
A
′
(AB)' = B'A'
(AB)′=B′A′。这个规则指出,两个矩阵相乘的结果的转置等于各自转置后反向乘的结果。
- 逆矩阵的转置
- 对于任意可逆矩阵
A
A
A,
(
A
−
1
)
′
=
(
A
′
)
−
1
(A^{-1})' = (A')^{-1}
(A−1)′=(A′)−1。这意味着矩阵的逆的转置等于矩阵的转置的逆。
参数根据损失函数的推导
在多元线性回归中,我们的目标是找到系数 β \beta β 的值,使得损失函数 S S S 的值最小。通过对 S S S 关于 β \beta β 求偏导并设为0,我们可以找到使 S S S 最小化的 β \beta β 的解析解,即:
S = ( Y − X β ) ’ ( Y − X β ) S = (Y - X\beta)’(Y - X\beta) S=(Y−Xβ)’(Y−Xβ)
上式可以转化为
S = Y ′ Y − Y ′ X β − β ′ X ′ Y + β ′ X ′ X β S = Y'Y - Y'X\beta - \beta'X'Y + \beta'X'X\beta S=Y′Y−Y′Xβ−β′X′Y+β′X′Xβ
注意到 Y ′ X β Y'X\beta Y′Xβ 是一个数(标量),因此它等于其自身的转置,即 Y ′ X β = ( Y ′ X β ) ′ = β ′ X ′ Y Y'X\beta = (Y'X\beta)' = \beta'X'Y Y′Xβ=(Y′Xβ)′=β′X′Y。所以,我们可以将 S S S 简化为:
S = Y ′ Y − 2 β ′ X ′ Y + β ′ X ′ X β S = Y'Y - 2\beta'X'Y + \beta'X'X\beta S=Y′Y−2β′X′Y+β′X′Xβ
接下来,我们对 β \beta β 求偏导
这里,我们需要注意的是, β ′ X ′ Y \beta'X'Y β′X′Y 是关于 β \beta β 的线性项,而 β ′ X ′ X β \beta'X'X\beta β′X′Xβ 是关于 β \beta β 的二次项。求偏导数时,线性项的导数是其系数,二次项的导数则需要应用链式法则。
这里,我们使用了以下的矩阵微分规则:
- 对于形式为 β ′ X ′ Y \beta'X'Y β′X′Y 的项,其对 β \beta β 的偏导数是 X ′ Y X'Y X′Y。
- 对于形式为
β
′
X
′
X
β
\beta'X'X\beta
β′X′Xβ 的项,其对
β
\beta
β 的偏导数是
2
X
′
X
β
2X'X\beta
2X′Xβ。
所以我们就可以得到:
∂ S ∂ β = − 2 X ′ Y + 2 X ′ X β \frac{\partial S}{\partial \beta} = -2X'Y + 2X'X\beta ∂β∂S=−2X′Y+2X′Xβ
根据这个公式就可以求出所有的 β \beta β,因为它是一个矩阵。
为了找到最小化 S S S 的 β \beta β 值,我们将偏导数设置为零,因为这是一个关于 β \beta β 的二次函数,且开口向上,所以偏导数为0的地方就是其极小值:
− 2 X ′ Y + 2 X ′ X β = 0 -2X'Y + 2X'X\beta = 0 −2X′Y+2X′Xβ=0
最后,我们解这个方程找到 β \beta β:
2 X ′ X β = 2 X ′ Y 2X'X\beta = 2X'Y 2X′Xβ=2X′Y
简化得到:
X ′ X β = X ′ Y X'X\beta = X'Y X′Xβ=X′Y
因此, β \beta β 的解析解是:
β = ( X ′ X ) − 1 X ′ Y \beta = (X'X)^{-1}X'Y β=(X′X)−1X′Y
这个解给出了系数 β \beta β 的值,它最小化了残差平方和 S S S。
所以在代码实现中我们就可以按照如上公式 β = ( X ′ X ) − 1 X ′ Y \beta = (X'X)^{-1}X'Y β=(X′X)−1X′Y求出所有的斜率 β 1 − β n \beta_1 - \beta_n β1−βn 以及截距 β 0 \beta_0 β0 。
接下来我么就来进行代码实现。
3. 代码实现
3.1 问题描述
现在有如下数据:
身高(cm) 年龄(岁) 性别 体重(kg) 170 30 男 75 160 45 女 65 180 25 男 85 165 35 女 70 175 40 男 80 155 50 女 60 185 28 男 90 168 32 女 68 172 37 男 78 163 42 女 72 178 29 男 83 167 31 女 66 现在我们有12个样本数据。每个样本都包括了身高、年龄和性别这三个自变量,以及相应的体重作为因变量。要求预测给定身高、年龄和性别这三个自变量后其对应的体重?
3.2 多元线性回归模型
通过前面的分析,我们可以得到多元线性回归模型的关于 β \beta β的计算公式:
β = ( X ′ X ) − 1 X ′ Y \beta = (X'X)^{-1}X'Y β=(X′X)−1X′Y
其中,X是自变量的矩阵,Y是因变量的矩阵。我们可以通过这个公式来计算出多元线性回归模型的系数。
这个公式中,X’是X的转置矩阵, ( X ′ X ) − 1 (X'X)^{-1} (X′X)−1是X’X的逆矩阵。
它是根据最小化误差平方和的原理推导出来的。
# 代码实现,导入numpy库,定义数据 import numpy as np X = np.array( [[170, 30, 1], [160, 45, 0], [180, 25, 1], [165, 35, 0], [175, 40, 1], [155, 50, 0], [185, 28, 1], [168, 32, 0], [172, 37, 1], [163, 42, 0], [178, 29, 1], [167, 31, 0]]) Y = np.array([75, 65, 85, 70, 80, 60, 90, 68, 78, 72, 83, 66])3.3 可视化数据
from pyecharts import options as opts from pyecharts.charts import Scatter3D data = X.tolist() # 转换数据为列表格式 # 创建3D散点图 scatter3D = Scatter3D(init_opts=opts.InitOpts(width="800px", height="600px")) scatter3D.add("", data) # 设置3D散点图的全局选项 scatter3D.set_global_opts( title_opts=opts.TitleOpts(title="3D Scatter Plot"), visualmap_opts=opts.VisualMapOpts( max_=1, min_=0, range_color=["#313695", "#4575b4", "#74add1", "#abd9e9", "#e0f3f8", "#ffffbf", "#fee090", "#fdae61", "#f46d43", "#d73027", "#a50026"], ) ) # 直接在Jupyter Notebook中显示图表 scatter3D.render_notebook()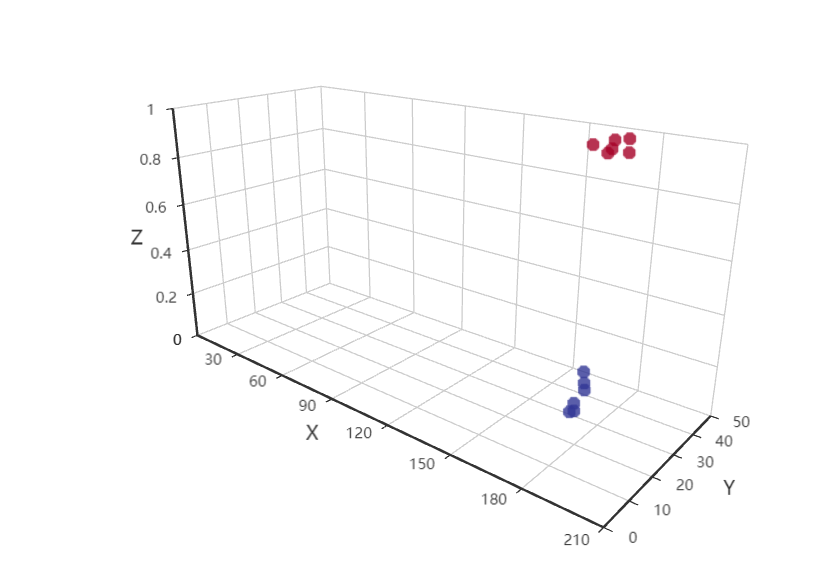
print(X.shape[0], X.shape[1], type(X.shape[0]), type(X.shape[1]))
12 3
# 根据公式计算beta(其中包括截距项) def multi_linear_regression(X, Y): # np.hstack()是将两个矩阵水平合并,比如: # np.hstack([np.array([[1, 2, 3]]), np.array([[4, 5, 6]])]) = np.array([[1, 2, 3, 4, 5, 6]]) # 这里是将X矩阵的第一列全部设置为1,用于计算截距项,X.shape[0]是X矩阵的行数 X = np.hstack([np.ones((X.shape[0], 1)), X]) # ------------------------------------------------ # 求解beta # np.linalg.inv()是求矩阵的逆 # np.dot()是矩阵乘法 # np.transpose()是矩阵转置 # \beta = (X'X)^{-1}X'Y # ------------------------------------------------ beta = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), Y) return beta# 计算beta beta = multi_linear_regression(X, Y) print(beta)
[-112.53822782 1.04161439 0.2448106 2.64148459]
3.4 回归方程为
Y = beta[0] + beta[1] * X1 + beta[2] * X2 + beta[3] * X3
其中X1、X2、X3分别是身高、年龄和性别
print("回归方程为:Y = {:.2f} + {:.2f} * X1 + {:.2f} * X2 + {:.2f} * X3".format(beta[0], beta[1], beta[2], beta[3]))回归方程为:Y = -112.54 + 1.04 * X1 + 0.24 * X2 + 2.64 * X3
3.5 预测
# 假设要预测的数据为:身高170cm,年龄35岁,性别男 X_test = np.array([170, 35, 1]) # 预测 Y_test = beta[0] + np.dot(X_test, beta[1:]) print("预测的体重为:{:.2f}kg".format(Y_test))预测的体重为:75.75kg
# 假设要预测的数据为:身高160cm,年龄40岁,性别女 X_test = np.array([160, 40, 0]) # 预测 Y_test = beta[0] + np.dot(X_test, beta[1:]) print("预测的体重为:{:.2f}kg".format(Y_test))预测的体重为:63.91kg
3.6 可视化回归平面——实际上是不可行的
- 为了更好理解不同个数自变量的图像,我们分别绘制一元一次方程和二元一次方程的图像,以便更好地理解。
# 对于一元一次方程 2x+1=0,我将展示它在二维坐标系中的直线图 # 对于二元一次方程 x+2y−3=0,我将展示它在三维坐标系中的平面图 import matplotlib.pyplot as plt import numpy as np # 设置图像大小 plt.figure(figsize=(12, 6)) # 子图1:一元一次方程 2x + 1 = 0 plt.subplot(1, 2, 1) x = np.linspace(-10, 10, 400) y = -0.5 * np.ones_like(x) # 解为x = -1/2 plt.plot(x, y, label='2x + 1 = 0') plt.title('one-variable linear equation') plt.xlabel('x') plt.ylabel('y') plt.axhline(0, color='black', linewidth=0.5) plt.axvline(0, color='black', linewidth=0.5) plt.grid(color='gray', linestyle='--', linewidth=0.5) plt.legend() # 子图2:二元一次方程 x + 2y - 3 = 0 plt.subplot(1, 2, 2) x = np.linspace(-10, 10, 400) y = (3 - x) / 2 plt.plot(x, y, label='x + 2y - 3 = 0') plt.title('two-variable linear equation') plt.xlabel('x') plt.ylabel('y') plt.axhline(0, color='black', linewidth=0.5) plt.axvline(0, color='black', linewidth=0.5) plt.grid(color='gray', linestyle='--', linewidth=0.5) plt.legend() plt.tight_layout() plt.show()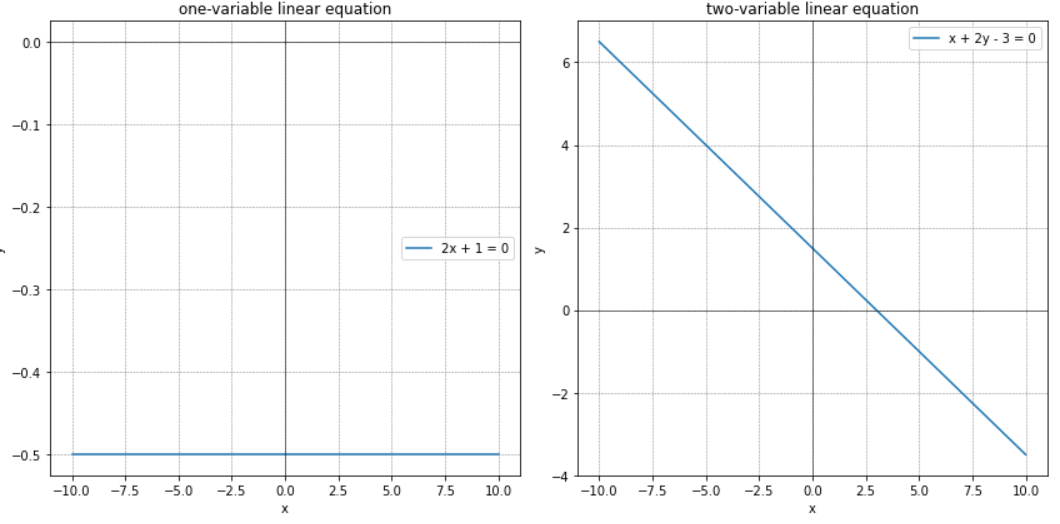
#假设只有两个自变量,我们可以绘制三维图像 import numpy as np import matplotlib.pyplot as plt # 定义原始数据点 X = np.array([ [170, 30, 1], [160, 45, 0], [180, 25, 1], [165, 35, 0], [175, 40, 1], [155, 50, 0], [185, 28, 1], [168, 32, 0], [172, 37, 1], [163, 42, 0], [178, 29, 1], [167, 31, 0] ]) # 回归方程的系数 coefficients = [-112.54, 1.04, 0.24, 2.64] # 生成X1, X2的网格 x1_range = np.linspace(150, 190, 20) x2_range = np.linspace(20, 50, 20) X1, X2 = np.meshgrid(x1_range, x2_range) # 重新计算回归平面的Y值,不考虑X3的影响 Y_plane = coefficients[0] + coefficients[1] * X1 + coefficients[2] * X2 # 创建3D图 fig = plt.figure() ax = fig.add_subplot(111, projection='3d') # 绘制原始数据点,使用X3值改变颜色 ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=X[:, 2], cmap='coolwarm', marker='o') # 绘制回归平面 ax.plot_surface(X1, X2, Y_plane, color='b', alpha=0.3) # 设置坐标轴标签 ax.set_xlabel('X1') ax.set_ylabel('X2') ax.set_zlabel('Y') plt.show()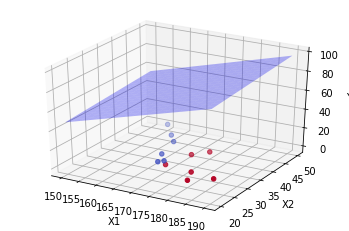
但是我们有三个自变量,这说明它构成的图像是一个三维的图像,我们无法在二维平面上展示出来。因此,我们无法通过图像来直观地理解多元线性回归模型。
3.7 模型评估——采用决定系数R方
计算公式为:
R 2 = 1 − ∑ i = 1 n ( Y i − Y i ^ ) 2 ∑ i = 1 n ( Y i − Y ˉ ) 2 R^2 = 1 - \frac{\sum_{i=1}^{n}(Y_i - \hat{Y_i})^2}{\sum_{i=1}^{n}(Y_i - \bar{Y})^2} R2=1−∑i=1n(Yi−Yˉ)2∑i=1n(Yi−Yi^)2
其中, Y i Y_i Yi是真实值, Y i ^ \hat{Y_i} Yi^是预测值, Y ˉ \bar{Y} Yˉ是真实值的均值。
R方的取值范围是0到1,R方越接近1,说明模型的拟合效果越好。
# 预测 Y_pred = beta[0] + np.dot(X, beta[1:]) print(Y_pred)
[74.52202148 65.136552 83.71411239 67.89651794 82.17819947 61.15253305 89.65661616 70.28692931 78.31892448 67.52696337 82.61012602 69.00050432]
# 计算R方 def r2_score(Y, Y_pred): return 1 - np.sum((Y - Y_pred) ** 2) / np.sum((Y - np.mean(Y)) ** 2) r2 = r2_score(Y, Y_pred) print("R方为:{:.2f}".format(r2))R方为:0.95
3.8 总结
- 多元线性回归模型是一种多元线性方程,它是通过多个自变量来预测因变量的一种模型。
- 通过结果来看,多元线性回归模型的R方为0.95,说明模型的拟合效果还是非常好的😂
- 为了更好理解不同个数自变量的图像,我们分别绘制一元一次方程和二元一次方程的图像,以便更好地理解。