不需要考虑mid+1、mid-1的二分查找模板，希望大家都能学会

文章目录

• 一、模板示范
• 二、模板
• 三、细节说明
• • 为什么L的初始值为-1，R的初始值为N
  • 为什么循环结束的条件是while(L+1!=R)?
  • 不会陷入死循环
  • 最后
  • 四、
  • •     例题one[数的范围](https://www.acwing.com/problem/content/791/)
    •     例题two[数的三次方根](https://www.acwing.com/problem/content/792/)
    • 五、相关学习的视频链接-[为啥二分查找容易出错](https://www.bilibili.com/video/BV1d54y1q7k7?spm_id_from=333.337.search-card.all.click)

      一、模板示范

          闫而总之，只要所要寻找的数组能够满足某一条件而被分成两边，就能进行二分，这边我们就拿有序数组的二分来做例子；

          假设目前有这么一组数据:1 2 2 3 3 4 下标从0开始

      

          假设此时的情景为，需要我们找到第一个>=3的数字，试想一下，如果能把整个区间分了两半，左边是=3的区间 如图:

      

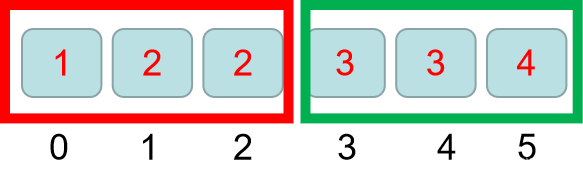
         那么右区间的第一个点，就是我们找到的符合>=3的第一个数字,将区间分为两半，是不是非常清晰！

         我先给出代码实现(不要害怕 马上就能见证奇迹)

      #include
      using namespace std;
      int main()
      {
      int a[6]={1,2,2,3,3,4};
      int l=-1,r=6;//定义两个指针
      while(l+1!=r)
      {
      	int mid=l+r>>1;//(相当于(l+r)/2)
      	if(a[mid]=3) r=mid;
      	else r=mid;		   //	 else l=mid;
      }
      cout
      	int mid=L+R1;
      	if(check()) L=mid;
      	else R=mid;
      	//最后根据你所分左右两边区间的结果
      	//选取L或者R作为结果
      }
      
          scanf("%d %d",&n,&m);
          for(int i=0;i
              int k;scanf("%d",&k);
              //寻找第一个等于K的坐标 我这边让二分的边界定为 左边为
                  int mid=l+r1;
                  //下面找第一个=5的坐标
                  if(q[mid]=k) r=mid;
                  else l=mid;
              }
              //此时得到的r是第一个>=5的坐标
              if(q[r]!=k) printf("-1 -1\n");
              else{
                  printf("%d ",r);
                      //现在找最后一个
                          
                          int mid=ll+rr>1;
                          if(q[mid]