目录
一、冒泡排序:
二、插入排序:
三、选择排序:
四、希尔排序:
五、堆排序:
六、快速排序:
6.1挖坑法:
6.2左右指针法
6.3前后指针法:
七、归并排序:
八、桶排序:
九、计数排序:
9.1绝对映射:
9.2现对映射:
十、基数排序:
一、冒泡排序:
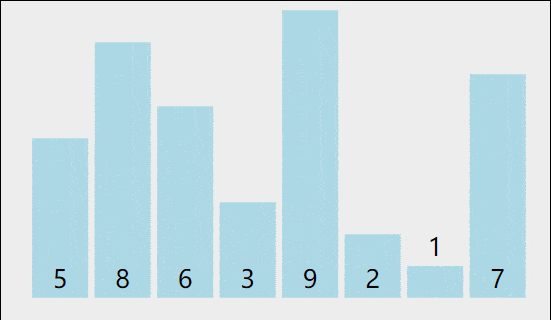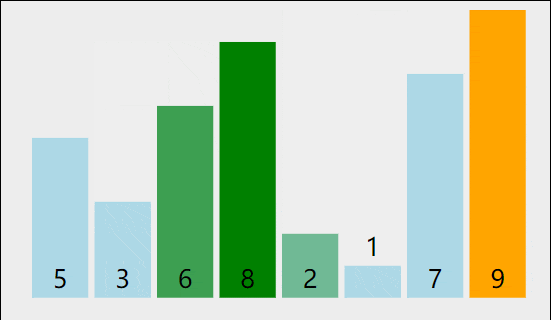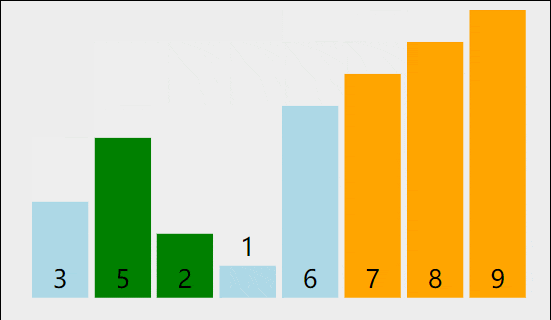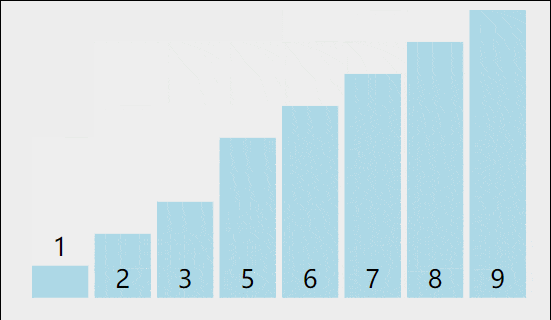
1、思路:通过对待排序序列从前向后(从下标较小的元素开始),依次对相邻两个元素的值进行两两比较,若发现前一个数大于后一个数则交换,使值较大的元素逐渐从前移向后部,就如果水底下的气泡一样逐渐向上冒。
2、先以一个数组讲解一下,然后再写代码:
待排序数组:3,9,-1,10,20
第一轮排序:
(1)3,9,-1,10,20 ----3跟9比较,不交换
(2)3,-1,9,10,20 ----9比 -1大,所以9跟 -1交换
(3)3,-1,9,10,20 ----9跟10比较,不交换
(4)3,-1,9,10,20 ----10跟20比较,不交换
第一轮过后,将20这个最大的元素固定到了最后的位置。
在第二轮的时候20不参与冒泡。
第二轮排序:
因为20的位置已经固定,所以只对前4个进行排序即可:
(1)-1,3,9,10,20 ----3比 -1大,进行交换
(2)-1,3,9,10,20 ----3跟9比较,不交换
(3)-1,3,9,10,20 ----9跟10比较,不交换
第二轮过后,将第二大的元素固定到了倒数第二个位置
第三轮排序:
10和20的位置已经确定,只需对前三个进行排序
(1)-1,3,9,10,20 ----3和-1比较,不交换
(2)-1,3,9,10,20 ----3和9比较,不交换
第三轮过后,将第三大的元素位置确定
第四轮排序:
只对前两个元素进行排序
(1)-1,3,9,10,20 ----3和-1比较,不交换
第四轮过后,将第四大的元素位置确定,此时总共5个元素,已经排序好4个,从而最后一个自然而然就是排好序的了
小结:
设总的元素个数为n,那么由上边的排序过程可以看出:
(1)总计需要进行(n-1)轮排序,也就是(n-1)次大循环
(2)每轮排序比较的次数逐轮减少
(3)如果发现在某趟排序中,没有发生一次交换, 可以提前结束冒泡排序
(4)时间复杂度是O(N^2) 在有序的时候,很快,因为有Exchange变量优化了代码
在乱序的时候很慢很慢。
#include
void swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//冒泡排序
void BubbleSort(int* a, int n)
{
int end = n - 1;//不能是n,不然会越界
while(end)
{
int exchange = 0;//优化,比较之后没有交换,说明已经排好了,就break循环
for (int i = 0; i
二、插入排序:
1、思路:
在待排序的元素中,假设前n-1个元素已有序,现将第n个元素插入到前面已经排好的序列中,使得前n个元素有序。按照此法对所有元素进行插入,直到整个序列有序。
但我们并不能确定待排元素中究竟哪一部分是有序的,所以我们一开始只能认为第一个元素是有序的,依次将其后面的元素插入到这个有序序列中来,直到整个序列有序为止。
2、举例:
如下图的插入扑克牌,当摸到7的时候,会不自觉的与前面的数比较,如果比7大,把大的数向后挪动(swap),然后在第一个小于7的后面插入7

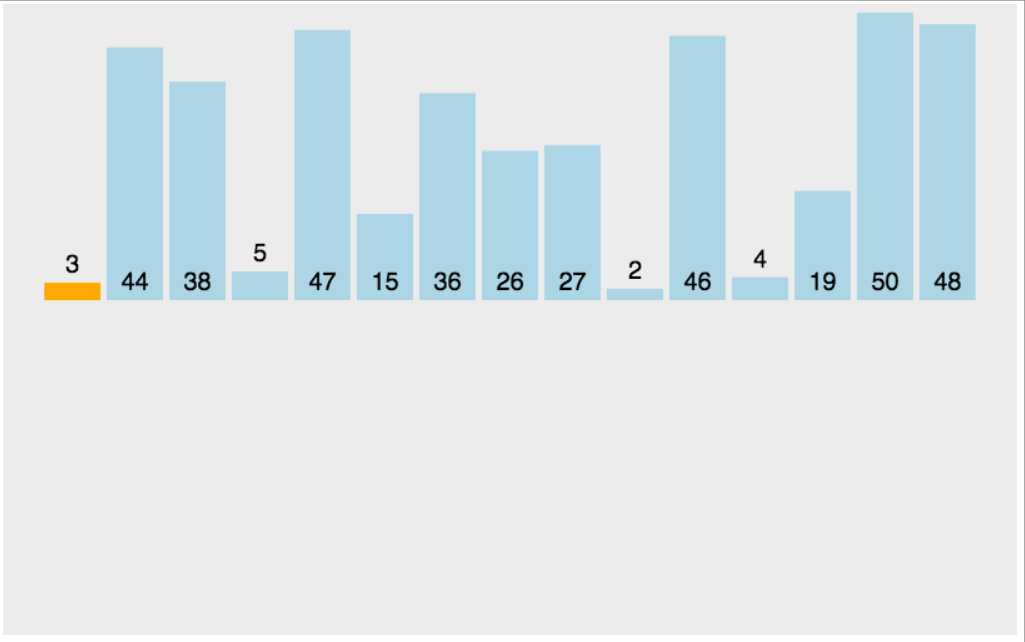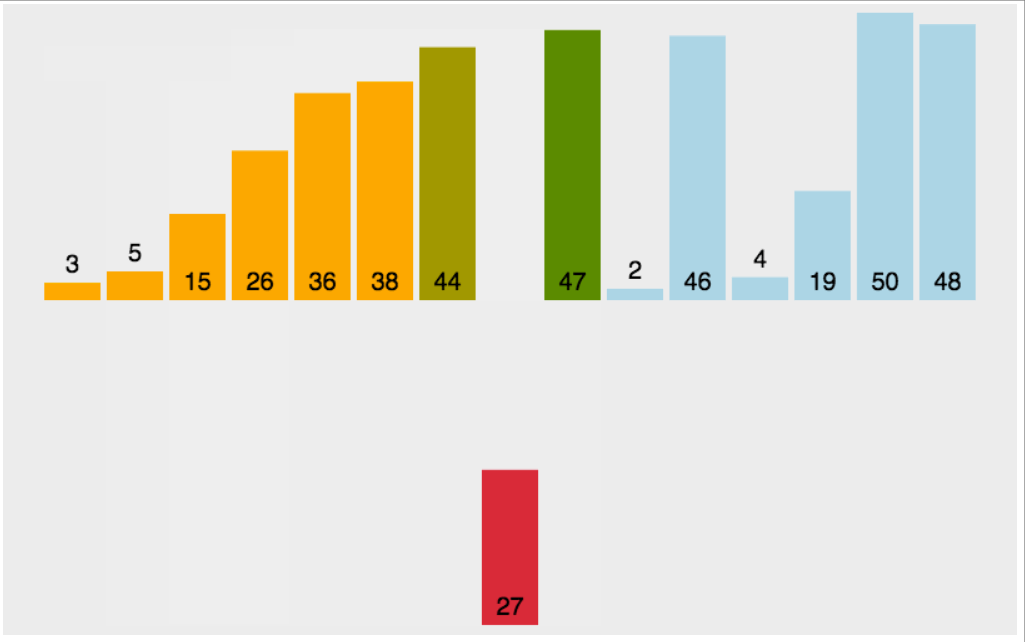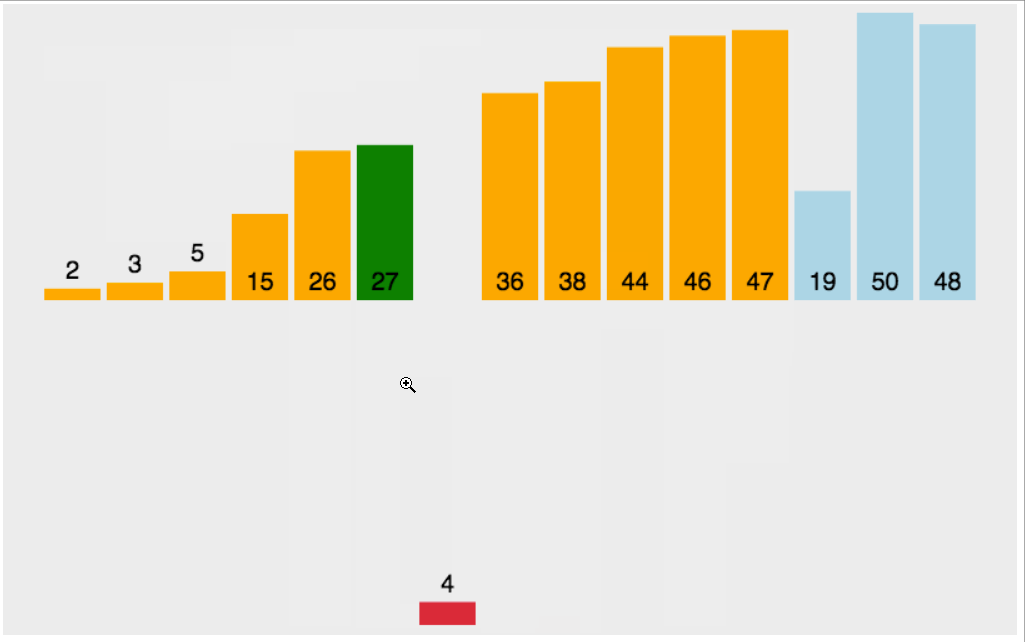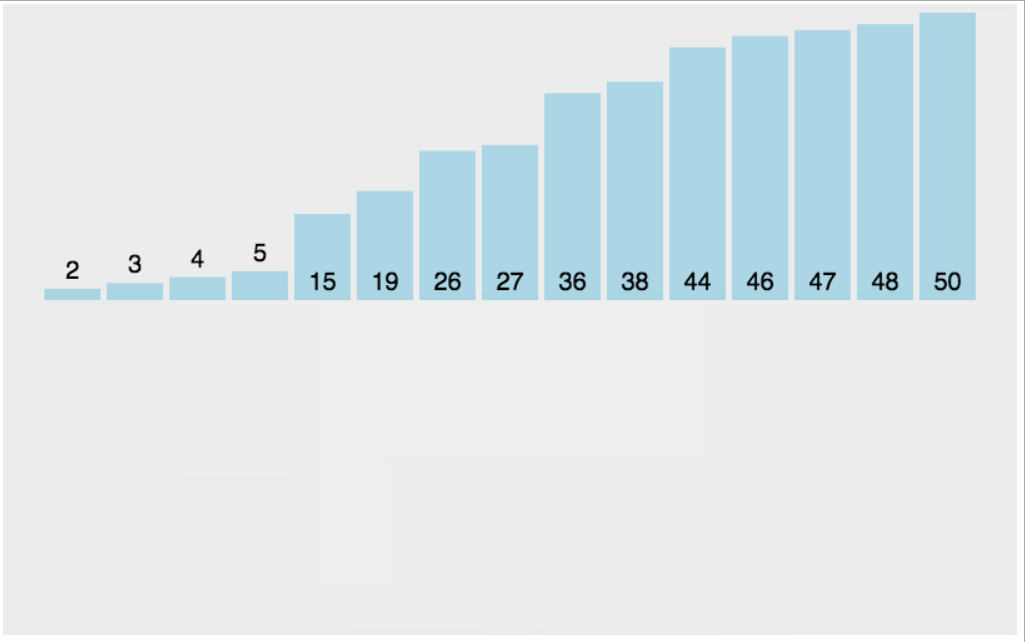
//插入排序
void InsertSort(int* a, int n)
{
for (int i = 1; i = 0 && a[j] >tmp; j--)
{
a[j+1] = a[j];
}
a[j+1] = tmp;
}
}
}
//两次循环就可以实现
//内部循环完成一趟的插入
//外层循环完成插入排序
三、选择排序:
思路:
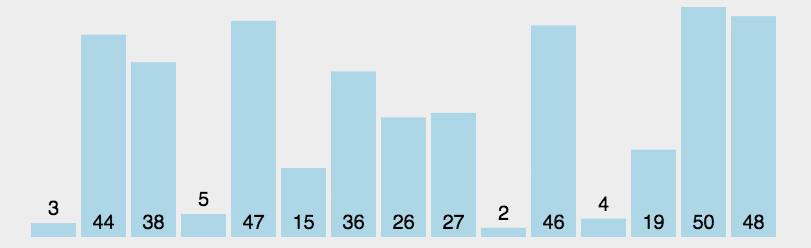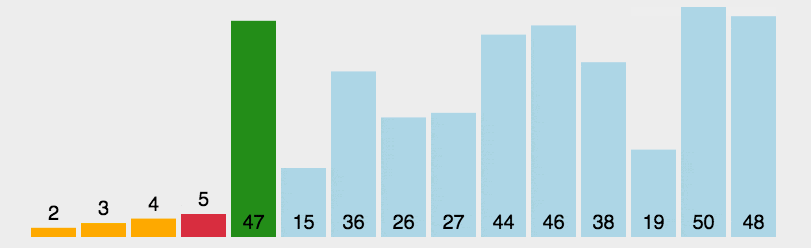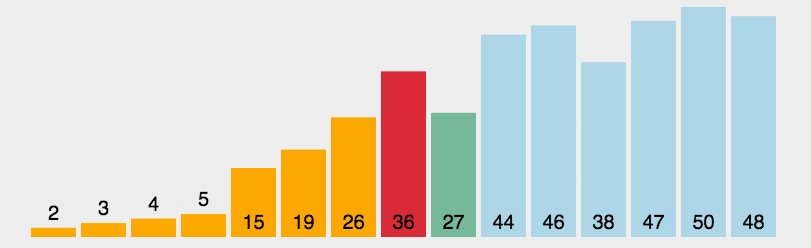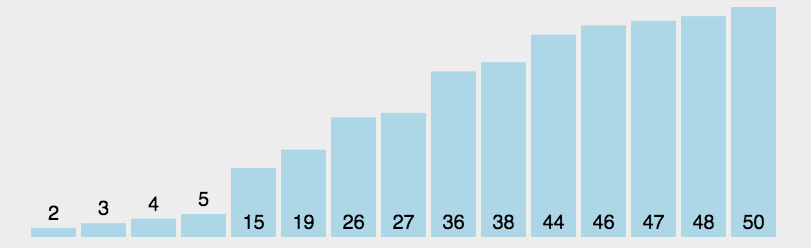
1.内层循环一趟找出最小值的下标,与第一个数交换。重复找小,交换的两个操作。
2.实际上,我们可以一趟选出两个值,一个最大值一个最小值,然后将其放在序列开头和末尾,这样可以使选择排序的效率快一倍。
但时间复杂度还是O(N^2),效率还是不高
//选择排序
void SelectSort(int* a, int n)
{
for (int i = 0; i = 0 && a[j] > tmp; j-=gap)//这里是j-=gap
{
a[j + gap] = a[j];
}
a[j + gap] = tmp;
}
}
}
}
五、堆排序:
先来认识堆:
1.什么是堆?
大堆:父亲大于儿子 小堆:父亲小于儿子(父亲,儿子是二叉树的概念)
2.堆的物理结构和逻辑结构?
物理结构:数组 逻辑结构:完全二叉树
堆排序包括建堆(向下调整+循环) 堆排序(交换+向下调整)
1.建堆:
要建大堆,堆顶的元素和最后一个数交换,然后把size--,就不会破坏堆的结构
2.向下调整算法:
比较两个孩子的大小,选出大的孩子,与父亲比较,如果孩子大于父亲,交换。然后把parent=child,child=parent*2+1;向下调整算法一共会调整h-1次

//向下调整算法(要满足它下面的都满足堆,才能用)
void AdjustDown(int* a, int n, int root)
{
int parent = root;
int child = parent * 2 + 1;
while (child a[parent])
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else break;
}
}
堆排序
void HeapSort(int* arr, int n)
{
//建大堆
//从最后一个根开始,就相当于它下面的都满足堆,就可以用向下调整算法
for (int i = (n-1-1)/2; i >= 0; i--)//n-1-1是因为数组的最后一个元素下标是n-1
{
AdjustDown(arr, n, i);
}
//排序
for (int i = n; i > 1; i--)
{
swap(&arr[0],&arr[i - 1]);
AdjustDown(arr, i-1, 0);
}
}
六、快速排序:
三种快排方法:(一定要自己尝试着去写,会有一些坑,自己写才可以体会)
1.挖坑法
2.左右指针法
3.前后指针法
6.1挖坑法:
1.思想:
记第一个数为key,要调整key的位置,使得左边的都要比key的小,右边的数都比key的大。
2.步骤:
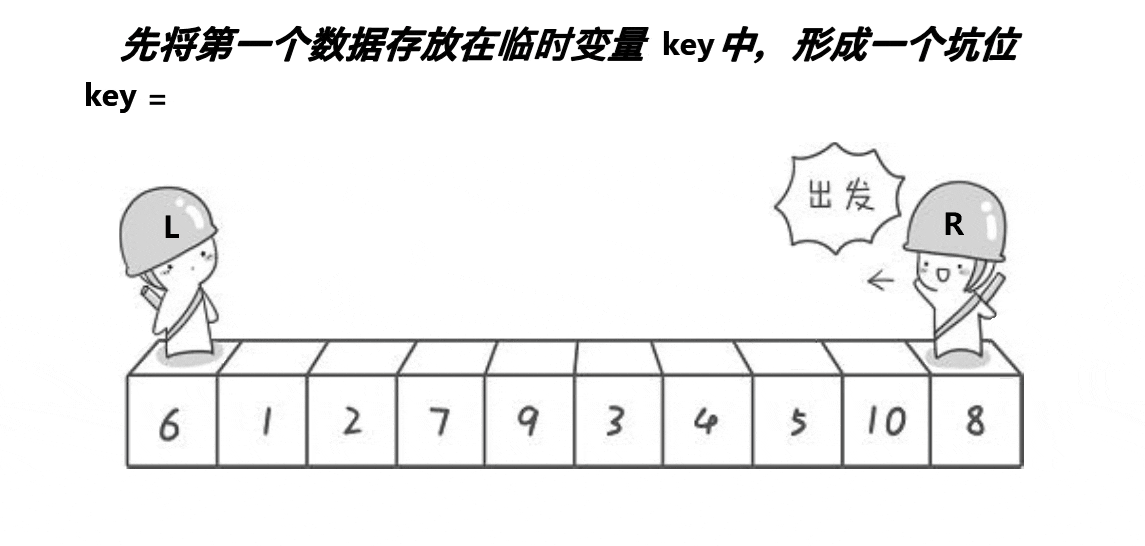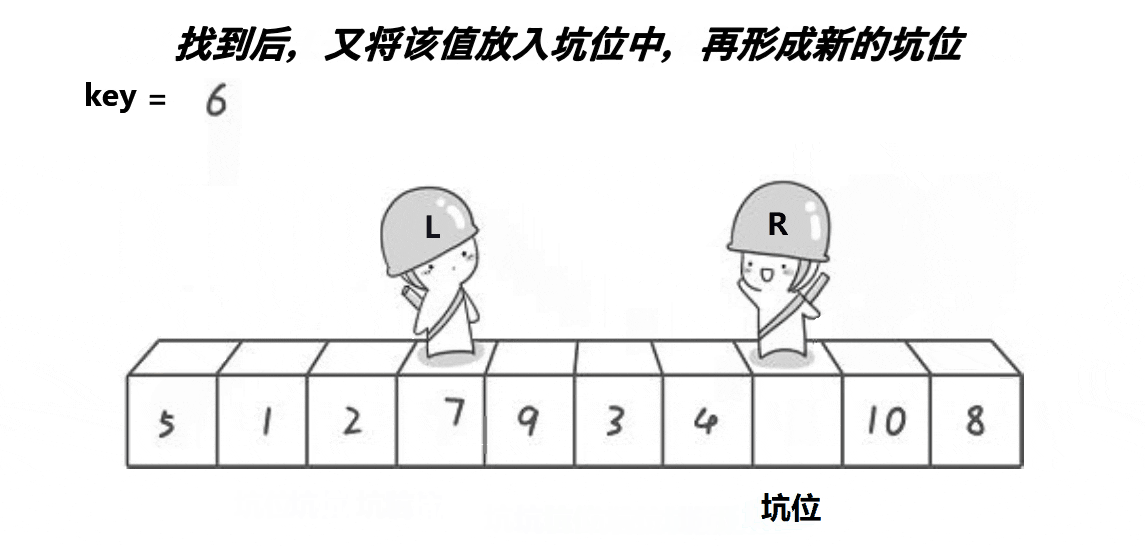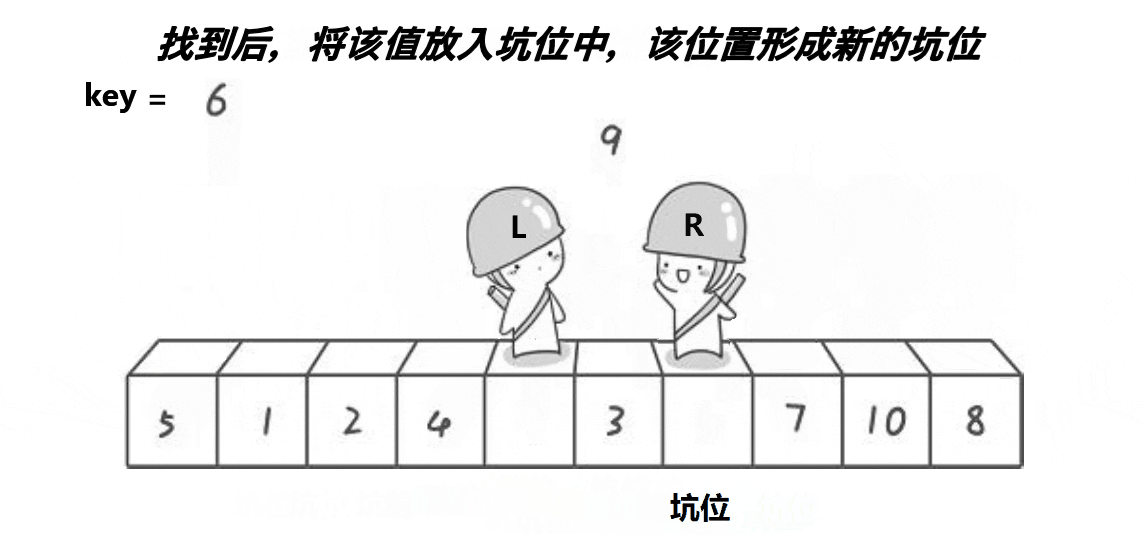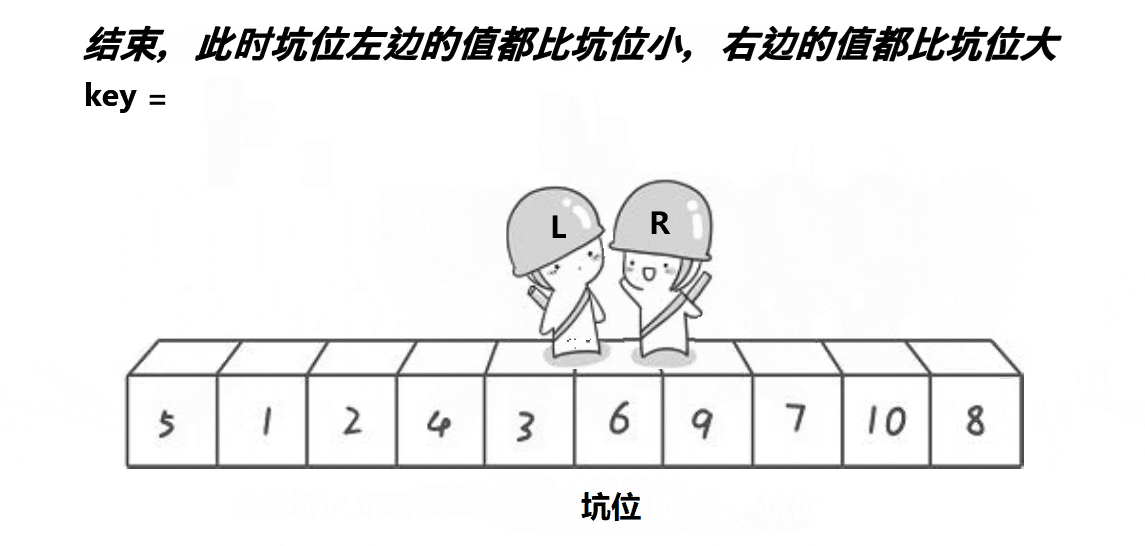
选出一个数据(一般是最左边或是最右边的)存放在key变量中,在该数据位置形成一个坑
还是定义一个left和一个right,left从左向右走(当遇到大于key的值时停下来)。right从右向左走(当遇到小于key的值时停下来)。(若在最左边挖坑,则需要right先走;若在最右边挖坑,则需要left先走)
把right的那个小的数放在坑中,在把left那个位置的值放在right那个位置中
重复操作,直到left>right时结束,完成一趟,把key放在了正确的位置
最后用分治思想,分成左边和右边,递归。
//1.挖坑法的快速排序
void QuickSort(int* a,int left,int right)
{
if (left >= right)//不能写成pivot==left,pivot-1与left不匹配,会报错
{
return;
}
int begin = left,end = right;
int key = a[begin];//挖了一个关键字
int pivot = begin;//挖了一个坑
while (begin = key)//在这里也要判断begin = a[key])
{
end--;
}
while (begin
{
reurn;
}//跳出递归
void QuickSort(int* a, int left,int right)
{
if (left >= right)
{
return;
}
int index=GetMidIndex(a,left, right);
swap(&a[left], &a[index]);
int key = left;
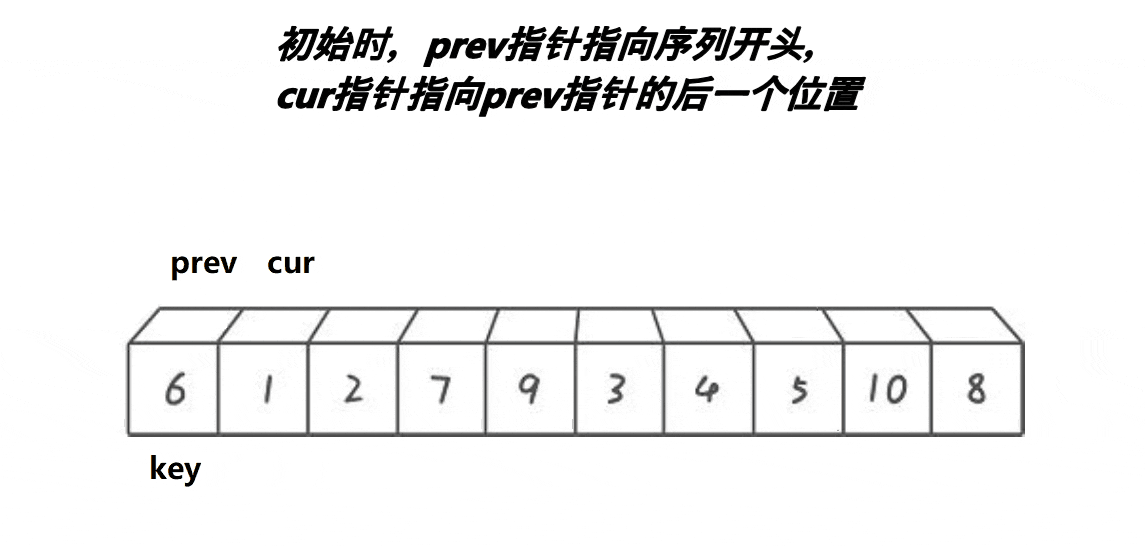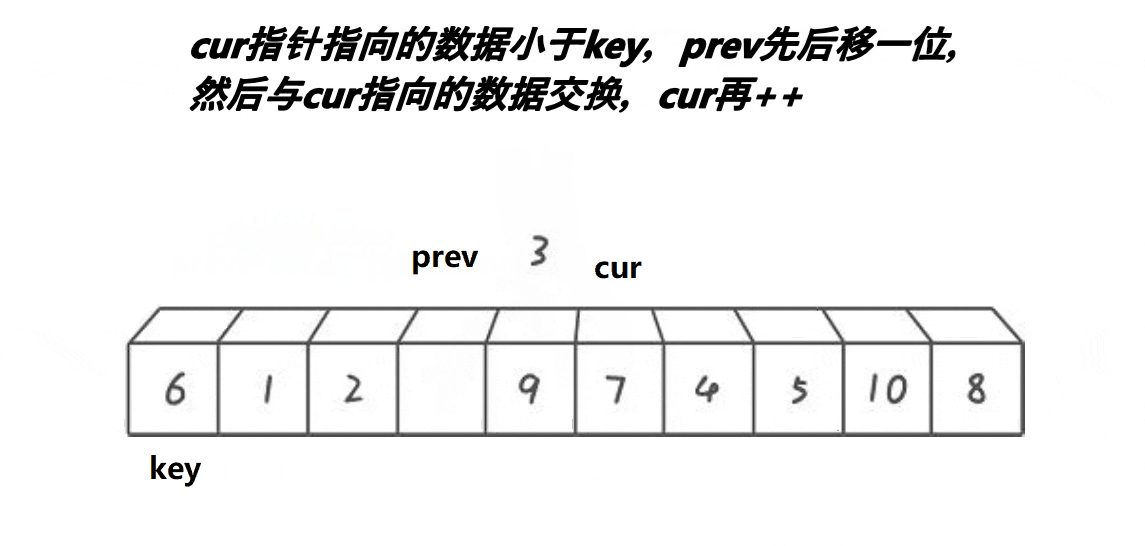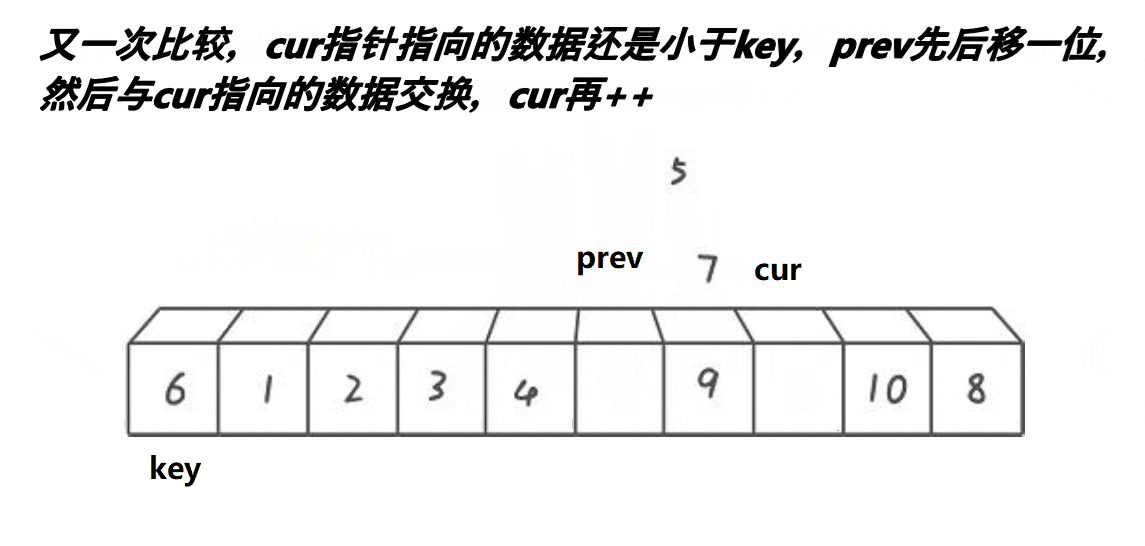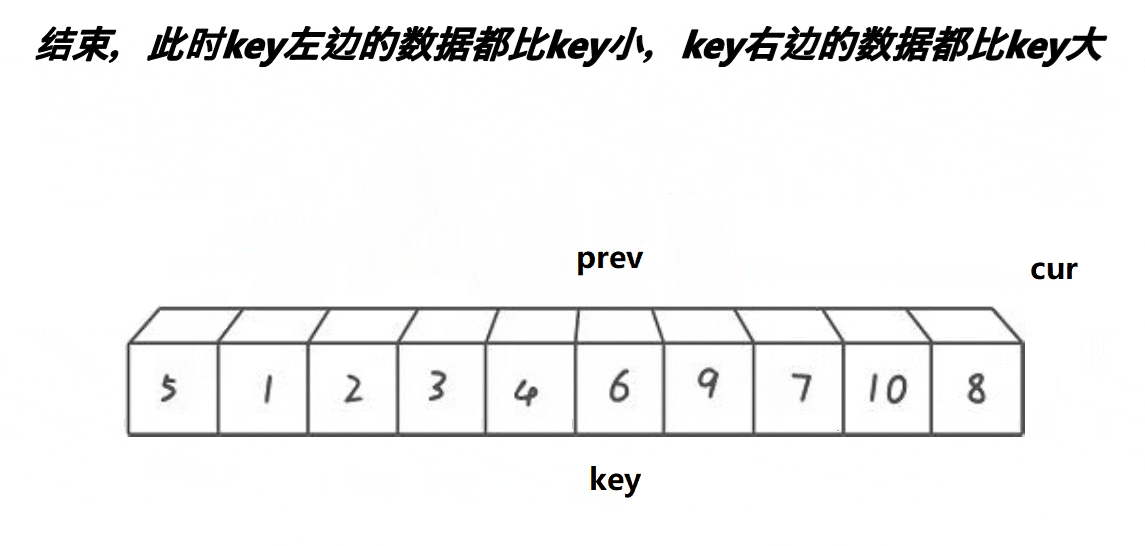
int prev = left;
int cur = left+1;
while (cur = a[left])
{
if (a[mid] = a[left])
{
return right;
}
else
{
return left;
}
}
}
else//a[left]>a[mid]
{
if (a[right] >= a[left])
{
return left;
}
else
{
if (a[right] >= a[mid])
{
return right;
}
else
{
return mid;
}
}
}
}
//交换
void swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//前后指针法
void QuickSort(int* a, int left,int right)
{
if (left >= right)
{
return;
}
int index=GetMidIndex(a,left, right);
swap(&a[left], &a[index]);
int key = left;
int prev = left;
int cur = left+1;
while (cur = right)
{
return;
}
int mid = (left + right) >> 1;
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid+1, right, tmp);
//合并
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int i = left;
while (begin1 next->num num)
{
p = p->next; //1.链表为空,p->next==NULL,进入不了循环
} //2.链表不为空,因为链表从无开始按顺序插入,数据为有序的,
//可以找到 前一个节点 next;
p->next = node;
(bucket_num[index]->num)++; //记录一下该链表中有几个有效节点
}
//打印结果
KeyNode * k = NULL; //定义一个空的结构体指针用于储存输出结果
for(i = 0;i next;k!=NULL;k=k->next)//通过最后一个指针指向空
k = bucket_num[i]->next;
for(int m=0;mnum;m++) //通过头指针记录节点数
{
printf("%d ",k->num);
k=k->next;
}
printf("\n");
}
九、计数排序:
一种特殊的排序,唯一种没有比较的排序(指没有前后比较,还是有交换的)
以数组的下标当做数值,有这个数的时候a[i]++;
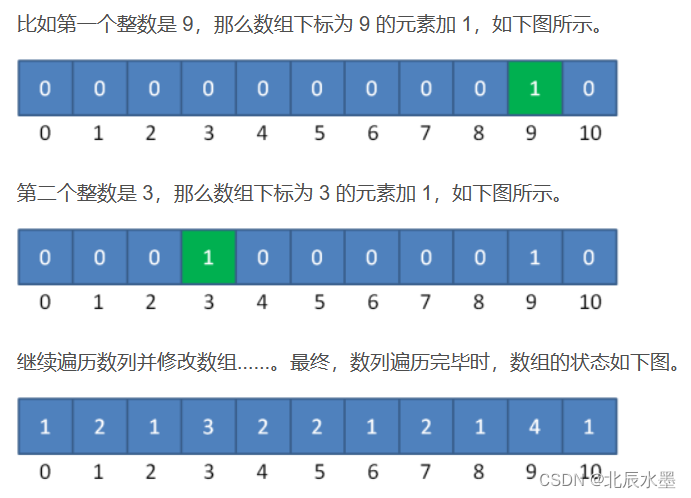
局限:适用于整数。数要求集中(否则空间的浪费大)
9.1绝对映射:
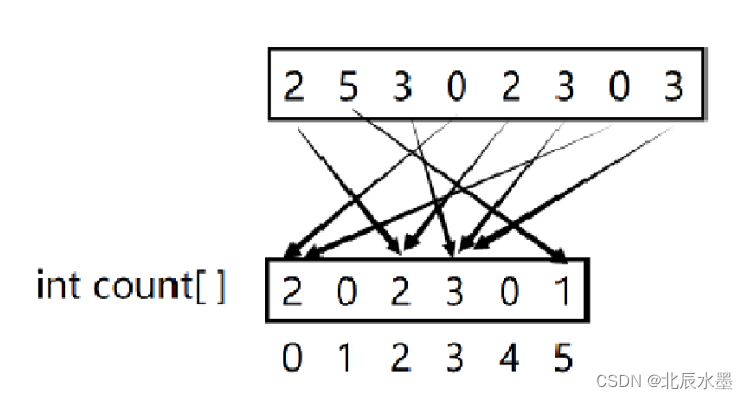
int * countingSort1(int arr[],int count,int max) {
int index = 0;
int *tmpArr = (int *)malloc(max*sizeof(int));
int *result = (int *)malloc(max*sizeof(int));
for(int k = 0;k 








