知识蒸馏（Knowledge Distillation）

知识蒸馏是做什么的？

知识蒸馏的概念由Hinton在Distilling the Knowledge in a Neural Network中提出，目的是把 一个大模型或者多个模型集成 学到的知识迁移到另一个轻量级模型上。

Knowledge Distillation，简称KD，顾名思义，就是将已经训练好的模型包含的知识(Knowledge)，蒸馏(Distill)提取到另一个模型里面去。

简而言之，就是模型压缩的一种方法，是一种基于“教师-学生网络思想”的训练方法。

做模型压缩的原因：一般情况下，我们在训练模型的时候使用了大量训练数据和计算资源来提取知识，但是大模型不方便部署到服务中去，一是因为大模型的推理速度慢，二是对设备的资源要求高，因此我们希望对训练好的模型进行压缩，在保证推理效果的前提下减小模型的体量。

····················································································································································································

插一句别的：我们可以从模型参数量和训练数据量之间的相对关系来理解underfitting和overfitting。在网上看到一个很形象的解释：模型就像一个容器，训练数据中蕴含的知识就像是要装进容器里的水。当数据知识量(水量)超过模型所能建模的范围时(容器的容积)，加再多的数据也不能提升效果(水再多也装不进容器)，因为模型的表达空间有限(容器容积有限)，就会造成underfitting；而当模型的参数量大于已有知识所需要的表达空间时(容积大于水量，水装不满容器)，就会造成overfitting，即模型的variance会增大(想象一下摇晃半满的容器，里面水的形状是不稳定的)。

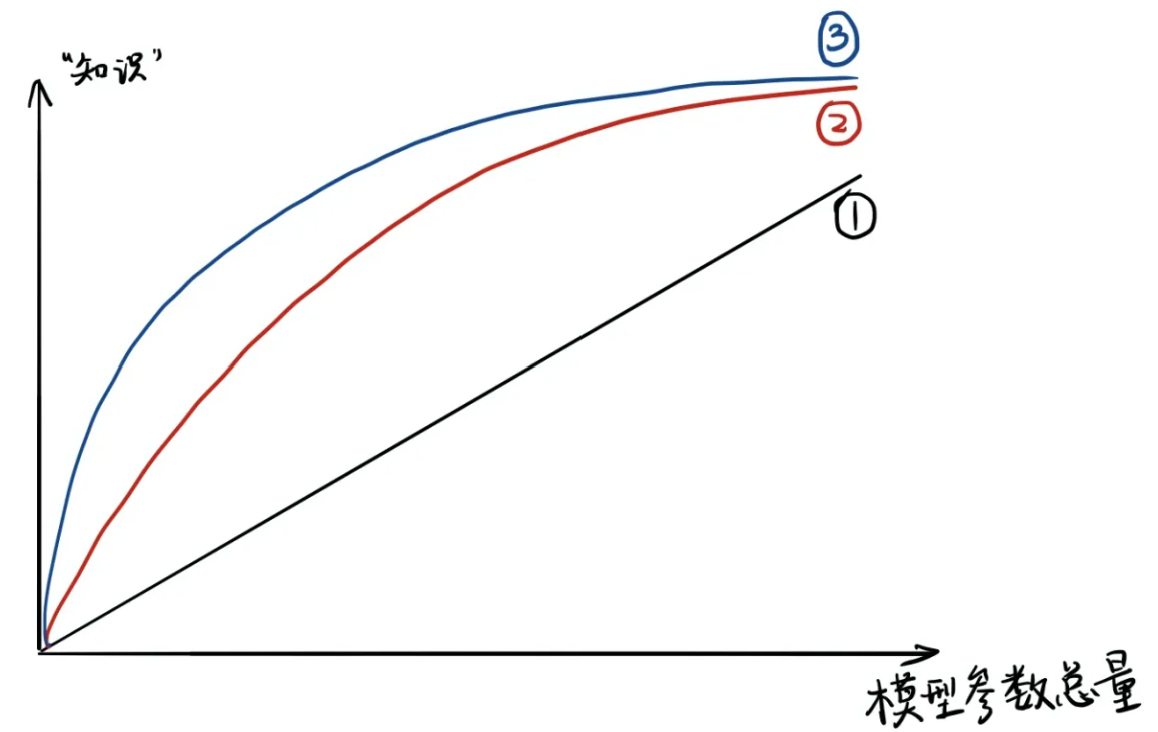
一个模型的参数量基本决定了其所能捕获到的数据内蕴含的“知识”的量。这个想法基本正确，但是要注意：

（1）模型的参数量和其所能捕获的“知识“量之间并非线性关系(下图中的1)，而是接近边际收益逐渐减少的一种增长曲线(下图中的2和3)

（2）完全相同的模型架构和模型参数量，使用完全相同的训练数据，能捕获的“知识”量并不一定完全相同，另一个关键因素是训练的方法。合适的训练方法可以使得在模型参数总量比较小时，尽可能地获取到更多的“知识”(下图中的3与2曲线的对比)。

图源：【经典简读】知识蒸馏(Knowledge Distillation) 经典之作

知识蒸馏的理论依据

下面介绍一下知识蒸馏所用到的理论依据。

名词解释

• Teacher：大而笨重的模型
• Student：小而紧凑的模型
• transfer set：用于小模型训练的数据，也是获得Teacher模型soft target输出的输入数据集
• hard target：样本原始标签
• soft target：Teacher模型输出的预测结果
• temperature：softmax函数中的超参数
• knowledge：可以理解为从输入向量到输出向量学习到的映射

  符号定义

  • z z z：Logits，模型去除输出层的输出。

    对于一般的分类问题，比如图片分类，输入一张图片后，经过深度神经网络各种非线性变换，在网络最后的Softmax层之前，会得到这张图片属于各个类别的大小数值 z i z_i zi​，某个类别的 z i z_i zi​数值越大，模型认为输入图片属于这个类别的可能性就越大。那么什么是Logits？这些汇总了网络内部各种信息后，得出的属于各个类别的汇总分值 z i z_i zi​就是Logits， i i i代表第 i i i个类别， z i z_i zi​代表属于第 i i i类的可能性。因为Logits不是概率值，所以一般在Logits数值上会用Softmax函数进行变换，得出的概率值作为最终分类结果概率。Softmax一方面把Logits数值在各类别之间进行概率归一，使得各个类别归属数值满足概率分布；另外一方面，它会放大Logits数值之间的差异，使得Logits得分两极分化，Logits得分高的得到的概率值更偏大一些，而较低的Logits数值，得到的概率值则更小。

  • p p p：probality，每个类的概率

    Teacher Model和Student Model

    知识蒸馏采取Teacher-Student模式：将复杂且大的模型作为Teacher，Student模型结构较为简单，用Teacher来辅助Student模型的训练，Teacher学习能力强，可以将它学到的知识迁移给学习能力相对弱的Student模型，以此来增强Student模型的泛化能力。复杂笨重但是效果好的Teacher模型不上线，就单纯是个导师角色，真正部署上线进行预测任务的是灵活轻巧的Student小模型。

    

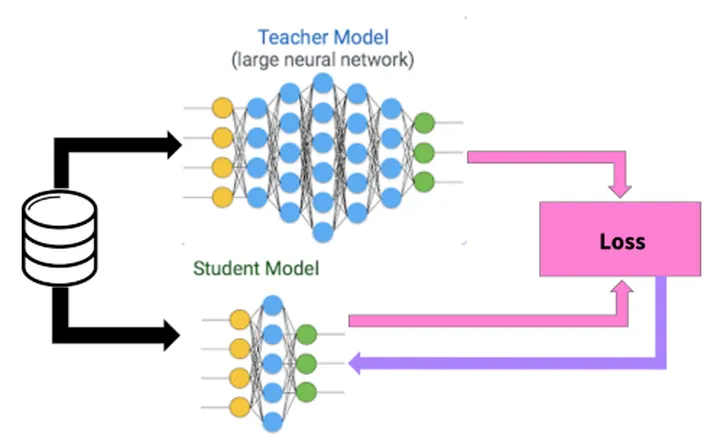
    需要注意的是，这里蒸馏的目的是小网络的概率分布趋近于大网络，而非单纯的正确率趋近于大网络。 Hinton注意到，虽然我们最终分类依靠的是softmax后的最大概率结果，但其实那些概率很小类之间的差别蕴含着网络进行特征提取的很多信息。例如，猫、狗、狮子三个类的输出分别是0.99,0.001,0.009，则很明显：狮子与猫的相似程度比狮子与狗高。

    因此，从理论上来说：只有小网络的所有大小输出与大网络都非常相近，才可以视为大小网络间概率分布非常接近。

    ---

    知识蒸馏分类

    知识蒸馏是对模型的能力进行迁移，根据迁移的方法不同可以简单分为基于目标蒸馏（也称为Soft-target蒸馏或Logits方法蒸馏）和基于特征蒸馏的算法两个大的方向，下面我们对其进行介绍。

    ···················································································································································································

    目标蒸馏-Logits方法

    目标蒸馏方法中最经典的论文就是来自于2015年Hinton发表的Distilling the Knowledge in a Neural Network。下面以这篇论文为例，讲一下目标蒸馏方法的原理。

    在这篇论文中，Hinton将问题限定在分类问题下，分类问题的共同点是模型最后会有一个softmax层，其输出值对应了相应类别的概率值。在知识蒸馏时，由于我们已经有了一个泛化能力较强的Teacher模型，在利用Teacher模型来蒸馏训练Student模型时，可以直接让Student模型去学习Teacher模型的泛化能力。一个很直白且高效的迁移泛化能力的方法就是：使用softmax层输出的类别的概率来作为“Soft-target” 。

    Hard-target 和 Soft-target

    【KD的训练过程和传统的训练过程的对比】

    • 传统的神经网络training过程：定义一个损失函数，目标是使预测值尽可能接近于真实值（Hard-target），损失函数就是使神经网络的损失值和尽可能小。这种训练过程是对ground truth求极大似然。
    • KD的training过程：是使用大模型的类别概率作为Soft-target的训练过程。

      

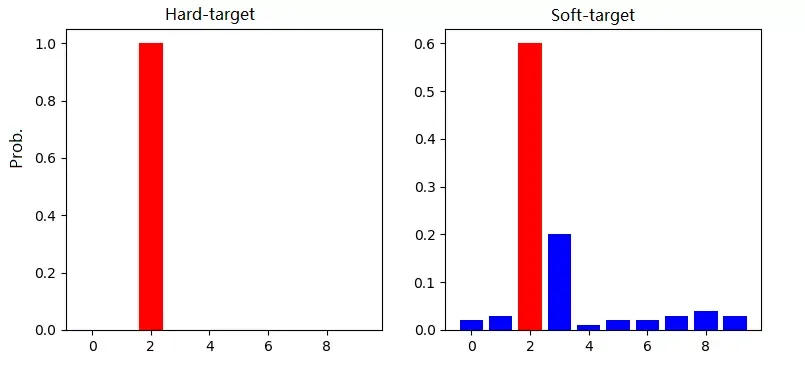
      从这张图可以看出：

      Hard-target：原始数据集标注的 one-shot 标签，除了正标签为 1，其他负标签都是 0。

      Soft-target：Teacher模型softmax层输出的类别概率，每个类别都分配了概率，正标签的概率最高。

      知识蒸馏用Teacher模型预测的 Soft-target 来辅助 Hard-target 训练 Student模型的方式为什么有效呢？

      softmax层的输出，除了正例之外，负标签也带有Teacher模型归纳推理的大量信息，比如某些负标签对应的概率远远大于其他负标签，则代表 Teacher模型在推理时认为该样本与该负标签有一定的相似性。而在传统的训练过程(Hard-target)中，所有负标签都被统一对待。也就是说，知识蒸馏的训练方式使得每个样本给Student模型带来的信息量大于传统的训练方式。

      如在MNIST数据集中做手写体数字识别任务，假设某个输入的“2”更加形似"3"，softmax的输出值中"3"对应的概率会比其他负标签类别高；而另一个"2"更加形似"7"，则这个样本分配给"7"对应的概率会比其他负标签类别高。这两个"2"对应的Hard-target的值是相同的，但是它们的Soft-target却是不同的，由此我们可见Soft-target蕴含着比Hard-target更多的信息。

      

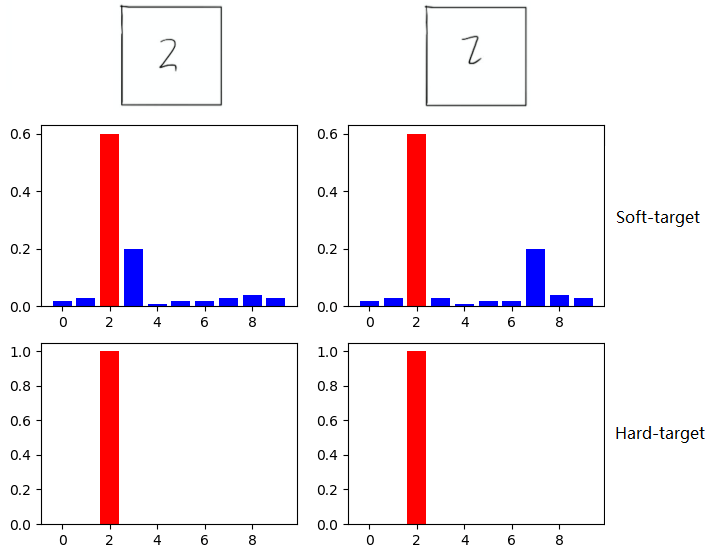
      在使用 Soft-target 训练时，Student模型可以很快学习到 Teacher模型的推理过程；而传统的 Hard-target 的训练方式，所有的负标签都会被平等对待。因此，Soft-target 给 Student模型带来的信息量要大于 Hard-target，并且Soft-target分布的熵相对高时，其Soft-target蕴含的知识就更丰富。同时，使用 Soft-target 训练时，梯度的方差会更小，训练时可以使用更大的学习率，所需要的样本也更少。这也解释了为什么通过蒸馏的方法训练出的Student模型相比使用完全相同的模型结构和训练数据只使用Hard-target的训练方法得到的模型，拥有更好的泛化能力。

      好模型的目标不是拟合训练数据，而是学习如何泛化到新的数据。所以蒸馏的目标是让student学习到teacher的泛化能力，理论上得到的结果会比单纯拟合训练数据的student要好。另外，对于分类任务，如果soft targets的熵比hard targets高，那显然student会学习到更多的信息。采用软标签的知识蒸馏方法，一方面压缩了模型，另一方面，增强了模型的泛化能力。

      知识蒸馏的具体方法

      神经网络使用 softmax 层来实现 logits 向类别概率（class probabilities）的转换。

      原始的softmax函数： q i = e x p ( z i ) ∑ j e x p ( z j ) q_i= \frac{exp(z_i)}{\sum_jexp(z_j)} qi​=∑j​exp(zj​)exp(zi​)​

      但是直接使用softmax层的输出值作为soft label，会有一个问题：当softmax输出的概率分布熵相对较小时，负标签的值都很接近0，对损失函数的贡献非常小，小到可以忽略不计。因此“温度”这个变量就派上了用场。

      加上temperature变量之后的softmax函数： q i = e x p ( z i / T ) ∑ j e x p ( z j / T ) q_i= \frac{exp(z_i/T)}{\sum_jexp(z_j/T)} qi​=∑j​exp(zj​/T)exp(zi​/T)​。其中， q i q_i qi​是每个类别输出的概率， z i z_i zi​是每个类别输出的logits， T T T是温度。当 T = 1 T=1 T=1时，就是标准的softmax公式。 T T T越高，softmax 的 output probability distribution 越趋于平滑，其分布的熵越大，负标签携带的信息会被相对地放大，模型训练将更加关注负标签。

      知识蒸馏训练的具体方法如下图所示，主要包括以下几个步骤：

      step1：训练好 Teacher 模型

      step2：利用高温 T h i g h T_{high} Thigh​产生 S o f t − t a r g e t Soft-target Soft−target

      step3：利用 { S o f t − t a r g e t Soft-target Soft−target, T h i g h T_{high} Thigh​} 和 { H a r d − t a r g e t Hard-target Hard−target, T = 1 T=1 T=1} 同时训练 Student 模型

      step4：设置 T = 1 T=1 T=1， Student 模型线上做推理（inference）

      

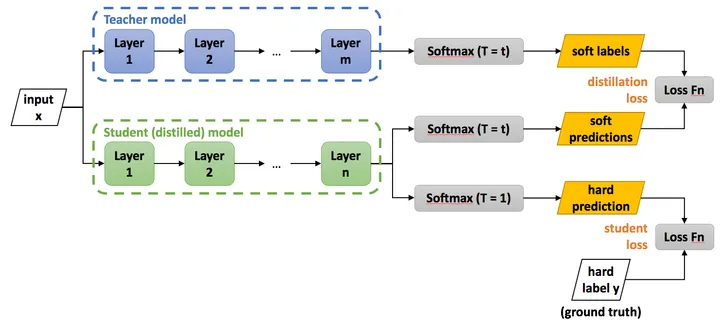
      训练Teacher的过程很简单，我们把step2和step3统一称为：高温蒸馏的过程。高温蒸馏过程的目标函数由distill loss(对应Soft-target)和Student loss(对应Hard-target)加权得到，即 L = α L s o f t + β L h a r d L=αL_{soft}+βL_{hard} L=αLsoft​+βLhard​ 。下面介绍一下具体的损失函数的两个部分：

      (1) Teacher模型和Student模型同时输入 transfer set (这里可以直接复用训练Teacher模型用到的training set)，用Teacher模型在高温 T h i g h T_{high} Thigh​下产生的softmax distribution来作为Soft-target，Student模型在相同温度 T h i g h T_{high} Thigh​条件（保证Student Model和Teacher Model的结果尽可能一致）下的softmax输出和Soft-target的cross entropy就是Loss函数的第一部分 L s o f t L_{soft} Lsoft​。

      具体形式为： L s o f t = − ∑ i N p i T l o g ( q i T ) L_{soft}=-\sum_{i}^Np_i^Tlog(q_i^T) Lsoft​=−∑iN​piT​log(qiT​) ，其中， p i T p_i^T piT​指 Teacher 模型在温度等于 T T T的条件下 softmax 输出在第 i i i类上的值。 q i T q_i^T qiT​指Student的在温度等于 T T T的条件下softmax输出在第 i i i类上的值。

      其中， p i T = e x p ( v i / T ) ∑ k N e x p ( v k / T ) p_i^T=\frac{exp(v_i/T)}{\sum_k^Nexp(v_k/T)} piT​=∑kN​exp(vk​/T)exp(vi​/T)​、 q i T = e x p ( z i / T ) ∑ k N e x p ( z j / T ) q_i^T=\frac{exp(z_i/T)}{\sum_k^Nexp(z_j/T)} qiT​=∑kN​exp(zj​/T)exp(zi​/T)​。其中， v i v_i vi​指 Teacher 模型的logits， z i z_i zi​指 Student 模型的logits， N N N指总标签数量。

      (2) Student模型在 T = 1 T=1 T=1的条件下（保证Student Model的结果和实际的类别标签尽可能一致）的softmax输出和ground truth的cross entropy就是Loss函数的第二部分 L h a r d L_{hard} Lhard​。

      具体形式为： L h a r d = − ∑ i N c i l o g ( q i 1 ) L_{hard}=-\sum_{i}^Nc_ilog(q_i^1) Lhard​=−∑iN​ci​log(qi1​) ，其中， c i c_i ci​指在第 i i i类上的ground truth值， c i ∈ { 0 , 1 } c_i∈\lbrace{0,1}\rbrace ci​∈{0,1}，正标签取1，负标签取0。

      其中， q i 1 = e x p ( z i ) ∑ k N e x p ( z k ) q_i^1=\frac{exp(z_i)}{\sum_k^Nexp(z_k)} qi1​=∑kN​exp(zk​)exp(zi​)​

      第二部分Loss 的必要性其实很好理解：Teacher模型也有一定的错误率，使用 ground truth 可以有效降低错误被传播给Student模型的可能性。打个比喻，老师虽然学识远远超过学生，但是他仍然有出错的可能，而这时候如果学生在老师传授的知识之外，可以同时参考到标准答案，就可以有效地降低被老师偶尔的错误“带偏”的可能性。

      最后， α α α和 β β β是关于 L s o f t L_{soft} Lsoft​和 L h a r d L_{hard} Lhard​的权重，实验发现，当 L h a r d L_{hard} Lhard​权重较小时，能产生最好的效果，这是一个经验性的结论。理论的推导不再给了，这里直接给出结论：由于 L s o f t L_{soft} Lsoft​贡献的梯度大约为 L h a r d L_{hard} Lhard​的 1 T 2 \frac{1}{T^2} T21​，因此在同时使用Soft-target和Hard-target的时候，需要在 L s o f t L_{soft} Lsoft​的权重上乘以 T 2 T^2 T2的系数，这样才能保证Soft-target和Hard-target贡献的梯度量基本一致。

      关于温度

      在知识蒸馏中，需要使用高温将知识“蒸馏”出来，但是如何调节温度呢，温度的变化会产生怎样的影响呢？

      

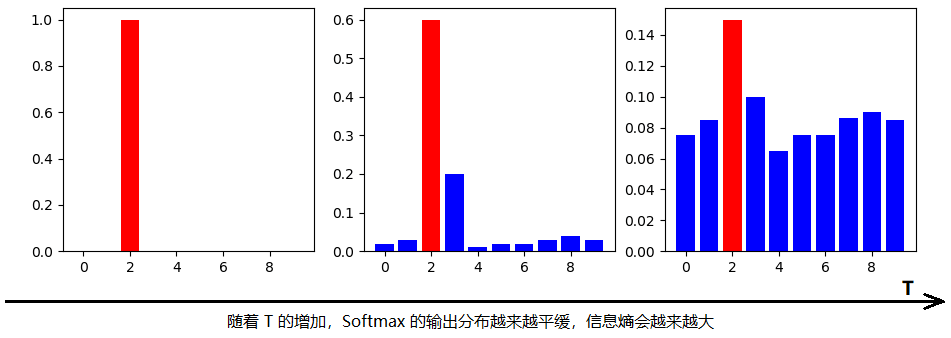
      温度 T T T有这样几个特点：

      • 原始的softmax函数是 T = 1 T=1 T=1时的特例； T