该内容需要有一定的数据结构基础,前置知识:二维前缀和、树状数组、线段树、扫描线等
二维数点的解法较多,可自行查找和学习其他解法
二维数点简介
二维数点又称二维偏序,它是这样一类问题,给出一个二维平面內的若干个点,多次询问某个矩形区域內包含多少个点(边界也算)。又或者,给一个长为 n n n 的序列,多次询问区间 [ l , r ] [l,r] [l,r] 中值在 [ x , y ] [x,y] [x,y] 内的元素个数。
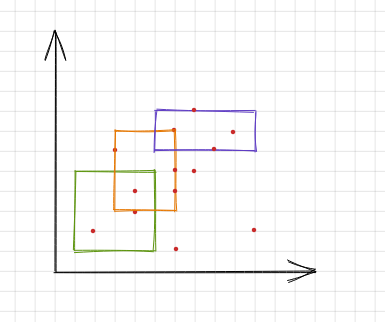
能解决这一问题的数据结构较多,包括树状数组/线段树、K-D Tree、可持久化线段树等,运用CDQ分治可解决更高维的偏序问题。以下着重讲解扫描线思想+树状数组解决二维偏序问题的方法。
二维数点的本质,是我们要查询一个矩形区域內的点数,首先考虑二维前缀和,对于矩形 ( x 1 , y 1 ) , ( x 2 , y 2 ) (x_1,y_1),(x_2,y_2) (x1,y1),(x2,y2),其二维前缀和为 s [ x 2 ] [ y 2 ] − s [ x 1 − 1 ] [ y 2 ] − s [ x 2 ] [ y 1 − 1 ] + s [ x 1 − 1 ] [ y 1 − 1 ] s[x_2][y_2]-s[x_1-1][y_2]-s[x_2][y_1-1]+s[x_1-1][y_1-1] s[x2][y2]−s[x1−1][y2]−s[x2][y1−1]+s[x1−1][y1−1]。可惜由于时空的双重限制,我们几乎不可能求出二维前缀和。
假设我们将矩形按横坐标排序,对于当前 x x x,如果所有 x ′ ≤ x x' \leq x x′≤x 的点的纵坐标都已知,那么将会有 s [ x ] [ y ] = q u e r y ( 1 , y ) s[x][y]=query(1,y) s[x][y]=query(1,y),其中 q u e r y ( 1 , y ) query(1,y) query(1,y) 代表查询纵坐标在 [ 1 , y ] [1,y] [1,y] 内的点数,这意味着我们把二维前缀和压成了一维的,每次查询只和 y y y 有关,这可以用简单数据结构来维护。整个思想与线段树的扫描线算法是十分相似的。
那么如何求出一个矩形区域內的答案呢?根据二维前缀和公式,我们只需要分别求出其四个区域的贡献(或正或负),相加即可。于是我们在从左往右沿 x x x 轴前进的过程中,不断将 x ′ ≤ x x' \leq x x′≤x 的点的纵坐标加入树状数组,依次求出所有询问对应的四个区域的贡献。询问需要提前离线,每个询问拆为四个区域。
于是,整个算法过程就是
- 将所有点按横坐标排序
- 将所有矩形询问拆成四个区域,即四次询问,所有询问按 x x x 轴排序
- 遍历询问,设当前横坐标为 x x x,保证 x ′ ≤ x x' \leq x x′≤x 的所有点的纵坐标已加入树状数组,在树状数组中查询答案,贡献加至原询问处
- 输出每个原询问的答案
练习
[SHOI2007]园丁的烦恼
题目链接
题意:平面上给出 n n n 个点, m m m 次询问,每次给出一个矩形,询问处于所给矩形区域內的点的数量。
思路:模板题,注意到 n , m n,m n,m 数据范围较大,离散化带个log容易被卡,而坐标范围为 [ 0 , 1 0 7 ] [0,10^7] [0,107],其实可以不进行离散化,但是由于坐标范围到0,树状数组不支持0下标,不妨将坐标全部加1。
参考代码:
#include using namespace std; constexpr int MAXN = 1e7 + 5; int sum[MAXN], ans[MAXN]; vector vec; vector q; inline int lowbit(int x) { return x & (-x); } void add(int pos, int x) { for (; pos 0; pos -= lowbit(pos)) ans += sum[pos]; return ans; } int main() { ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int n, m, x1, x2, y1, y2; cin >> n >> m; for (int i = 0; i > x1 >> y1, ++x1, ++y1; vec.emplace_back(x1, y1); } sort(vec.begin(), vec.end()); for (int i = 0; i > x1 >> y1 >> x2 >> y2; ++x1, ++y1, ++x2, ++y2; q.emplace_back(x1 - 1, y1 - 1, 1, i); q.emplace_back(x1 - 1, y2, -1, i); q.emplace_back(x2, y1 - 1, -1, i); q.emplace_back(x2, y2, 1, i); } sort(q.begin(), q.end()); int cur = 0; for (auto [x, y, c, id] : q) { while (cur > m; for (int i = 0; i > x1 >> y1 >> p; yy.push_back(y1); vec.emplace_back(x1, y1, p); } sort(vec.begin(), vec.end()); for (int i = 0; i > x1 >> y1 >> x2 >> y2; yy.push_back(y1 - 1), yy.push_back(y2); q.emplace_back(x1 - 1, y1 - 1, 1, i); q.emplace_back(x1 - 1, y2, -1, i); q.emplace_back(x2, y1 - 1, -1, i); q.emplace_back(x2, y2, 1, i); } sort(q.begin(), q.end()); sort(yy.begin(), yy.end()); yy.erase(unique(yy.begin(), yy.end()), yy.end()); int cur = 0; for (auto [x, y, c, id] : q) { y = lower_bound(yy.begin(), yy.end(), y) - yy.begin() + 1; while (cur x) break; _y = lower_bound(yy.begin(), yy.end(), _y) - yy.begin() + 1; add(_y, p), ++cur; } ans[id] += c * query_presum(y); } for (int i = 0; i a; vec.emplace_back(i, pre[a] ? pre[a] : 2), pre[a] = i; } sort(vec.begin(), vec.end()); cin >> m; for (int i = 0; i > l >> r, l += 2, r += 2; q.emplace_back(l - 1, 1, 1, i); q.emplace_back(l - 1, l - 1, -1, i); q.emplace_back(r, 1, -1, i); q.emplace_back(r, l - 1, 1, i); } sort(q.begin(), q.end()); int cur = 0; for (auto [x, y, c, id] : q) { while (cur y i b_k>y_i bk>yi 的怪物。求最大收益(可能为负)。思路:题目已经给出了二维偏序关系,设 x x x 轴和 y y y 轴分别表示攻击力和防御力,以怪物作为点,可以发现询问是武器和防具任意组合后,以 ( 0 , 0 ) , ( b k − 1 , a k − 1 ) (0,0),(b_k-1,a_k-1) (0,0),(bk−1,ak−1) 为顶点的一个矩形。枚举武器降掉一维,逐个加点,问题变成每次对于所有防具,求最大收益。
这需要使用线段树来维护,先设定 [ 1 , 1 0 6 ] [1,10^6] [1,106] 內所有防具的初始收益,每次加点相当于给 [ y i + 1 , 1 0 6 ] [y_i+1,10^6] [yi+1,106] 内的所有防具增加 z i z_i zi 的收益,查询全局最值并更新答案即可。
参考代码:
#include using namespace std; constexpr int MAXN = 1e6 + 5, N = 1e6 + 1; int mx[MAXN mx[rt if (L mx[rt] += C, add[rt] += C; return; } int mid = (l + r) 1; pushDown(rt); if (L if (L ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int n, m, p, x, y, z; cin n m p; for (int i = 1; i y, w[x] = max(w[x], -y); for (int i = 1; i x >> y >> z, mon.emplace_back(x, y, z); // sort(weapon.begin(), weapon.end()); sort(mon.begin(), mon.end()); int cur = 0, ans = -2e9; for (auto [a, ca] : weapon) { while (cur = a) break; modify(y + 1, N, z, 1, N, 1), ++cur; } ans = max(ans, -ca + query(1, N, 1, N, 1)); } cout return x & (-x); } void add(int pos, int x) { for (; pos n >> m; for (int i = 1, x, y; i > x >> y; G[x].push_back(y), G[y].push_back(x); } dfs(1, 0); int lst = 1e5 + 2, cnt = 0; for (int i = 1, op, x; i cin > op >> x; if (op == 1) lst = x; else { ++cnt; q.emplace_back(L[x] - 1, lst - 1, 1, cnt); q.emplace_back(L[x] - 1, 1e5 + 4, -1, cnt); q.emplace_back(R[x], lst - 1, -1, cnt); q.emplace_back(R[x], 1e5 + 4, 1, cnt); } } sort(q.begin(), q.end()); int cur = 1; for (auto [x, y, c, id] : q) { while (cur








