2019年五一杯数学建模B题木板最优切割方案解题全过程文档及程序

2019年五一杯数学建模

B题 木板最优切割方案

原题再现

  徐州某家具厂新进一批木板如表 1 所示，在家具加工的过程中，需要使用切割工具生产表 2所示的产品。假设：木板厚度和割缝宽度忽略不计。

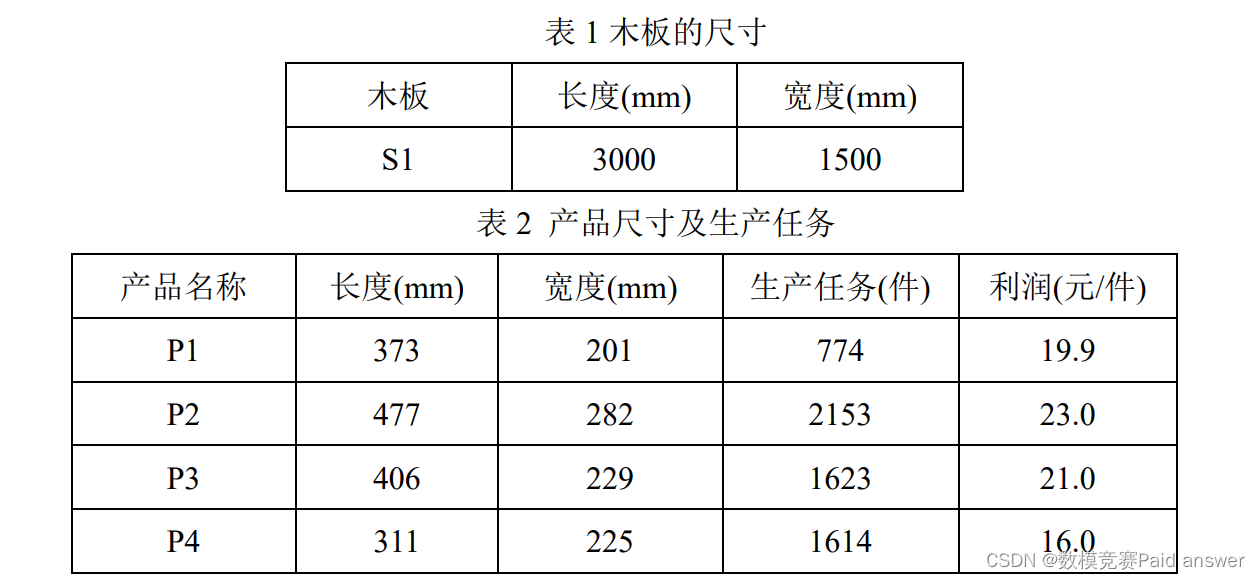
  请为该家具厂给出如下问题的木板最优切割方案。

  1. 在一块木板上切割 P1 产品，建立数学模型，给出木板利用率最高(即剩余木板面积最小)的切割方案，并将最优方案的结果填入表 3。

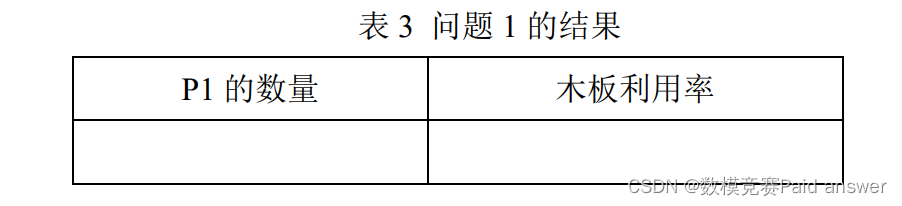
  2. 在一块木板上切割 P1 和 P3 产品，建立数学模型，给出按照木板利用率由高到低排序的前 3 种切割方案，并将结果填入表 4。

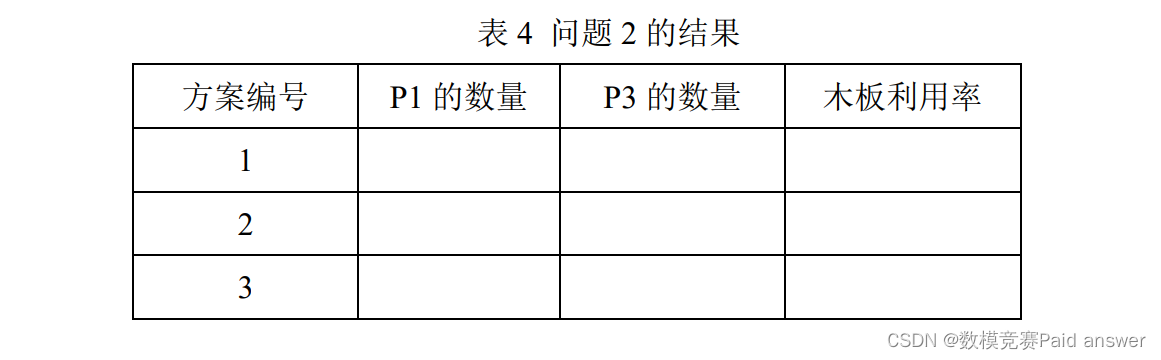
  3. 需要完成表 2 中 P1 和 P3 产品的生产任务，建立数学模型，给出木板总利用率最高的切割方案，并将结果填入表 5。

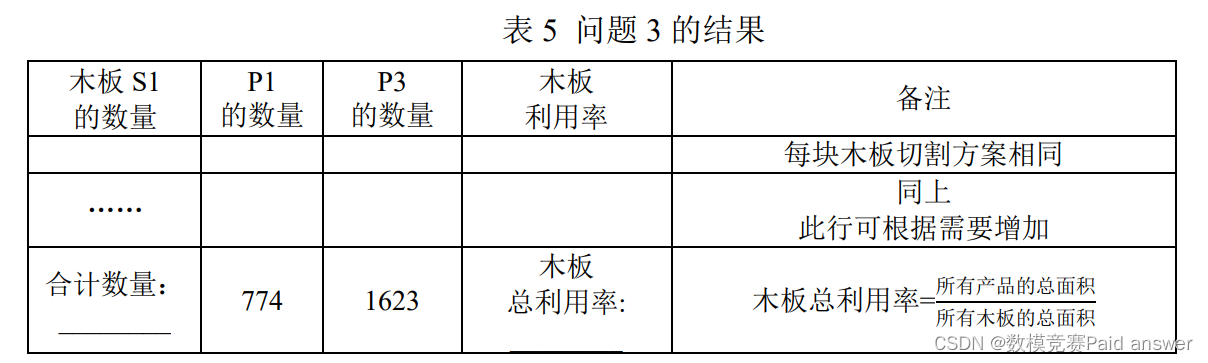
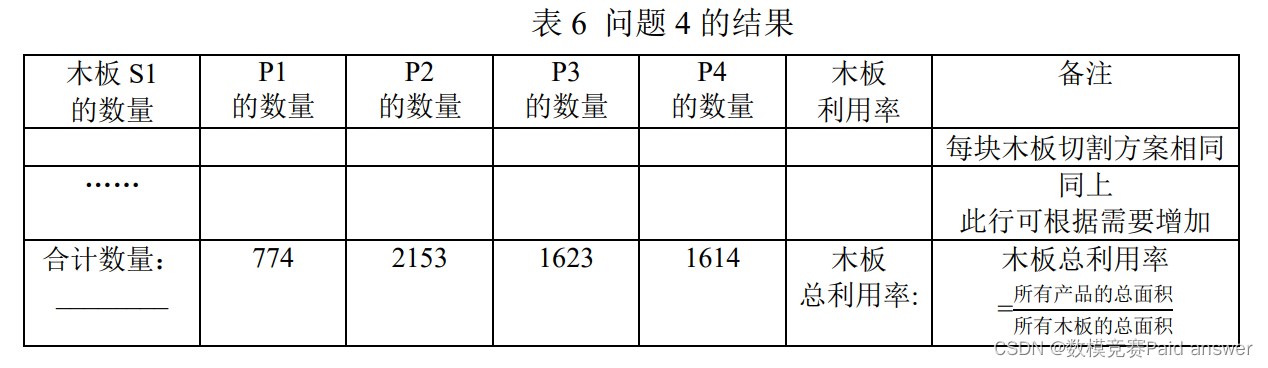
  4. 需要完成表 2 中 P1、P2、P3、P4 产品的生产任务，建立数学模型，给出木板总利用率最高的切割方案，并将结果填入表 6。

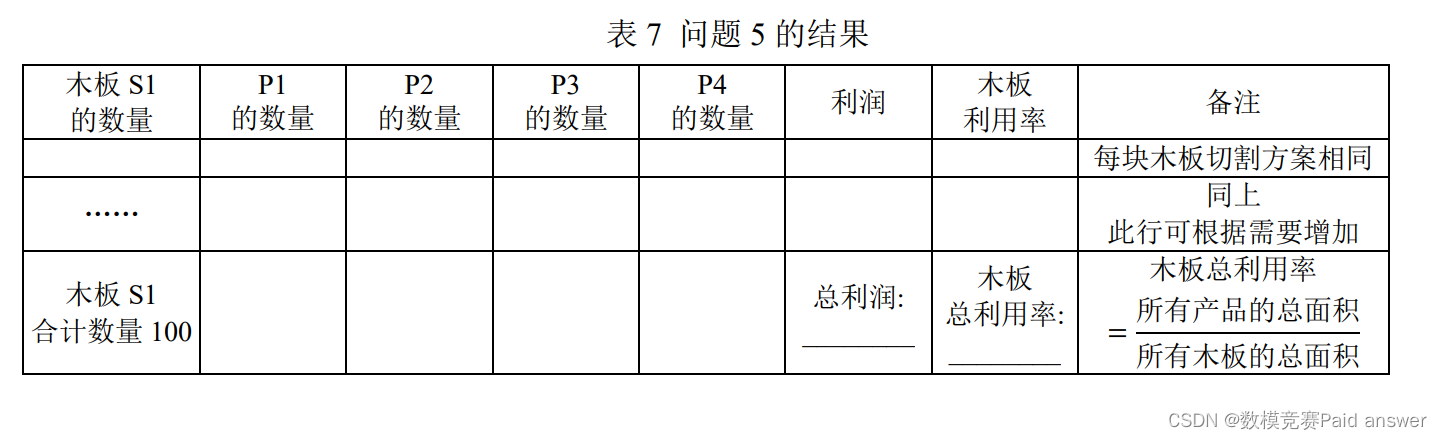
  5. 不考虑产品P1，P2，P3，P4的需求数量，给定100张S1木板，按照表2中给出的利润，建立数学模型，给出总利润最大的切割方案，并将结果填入表7。

整体求解过程概述(摘要)

  本文主要研究了在给定条件下如何对木板最优切割问题，重点研究分析了不同情况下的切割方案，通过建立线性规划模型和混合整数规划模型，并利用 MATLAB和 LINGO 对提出的模型进行求解，具体结果如下：

  对于问题一：考虑到只切割 P1 产品，若想木板利用率最高，只需切割产品的总面积最大，根据两个产品不能重叠，引入了坐标的思想，建立线性规划模型，结合 MATLAB 里的 fmincon 函数求解，得出：在只切割 P1 产品时，一块木板上能够切割 59 块 P1 产品，最高木板利用率为 98.30%。

  对于问题二：在问题一模型的基础上，添加变量𝑘𝑖表示产品种类，建立新的线性规划模型，结合遗传算法求解，在两种产品数量可以为 0 的情况下，木板利用率由高到底排序的前三种切割方案为：

  方案1：在木板全部切割P3产品，能够切割48 块P3，此时木板利用率为99.17%；

  方案2：在木板上切割47块P3产品和 1块P1 产品，此时木板利用率为98.77%；

  方案3：在木板上切割46块P3产品和 2块P1 产品，此时木板利用率为98.37%。

  对于问题三：根据问题一、二中提出的线性规划模型，对问题 3 分析并建立新的整数规划模型，得到最优切割方案如下：用 33 个木板全部切割 P3，得到 1584 个P3，剩余 39 个，利用率为 99.17%；用 13 个木板全部切割 P1，得到 767 个 P1，剩余 7 个 P1，利用率为 98.30%；再将剩余的 7 个 P1 和 39 个 P3 用 1 个木板切割，利用率为 92.23%；所需木板总数量为 47，木板总利用率为 98.78%。

  对于问题四：首先考虑切割面积较大的产品，每次切割按面积大小依次切割，由于选取方案较多，只枚举部分切割方案，以切割的木板数量最少为目标函数，建立混合整数规划模型。运用 LINGO 求解，得到结果：需要木板 S1 的总数量为 138，木板总利用率为 98.47%，具体方案见表 6。

  对于问题五：同问题 4 的思想相同，在分割时，首先考虑尽可能的切割单位面积利润较大的产品，即首先切割 P1 产品，建立线性规划模型，通过 LINGO 求解，得到结果：在 100 块木板上只切割 P1，总数量为 5900，其余产品数量均为 0，总利润为 117410 元，木板总利用率为 98.30%

  最后，深入研究了论文中提出的模型并加以分析，对模型的优化提供了一些改进思路。

模型假设：

  由于产品要求，需要对木板进行一定的打磨去除粗边的加工，切割后的木板也需要进行一定的加工处理才可投入使用。切割时需要考虑切割损失等影响因素，因此，对于本题，我们做出如下假设：

  （1） 不考虑切割时木板产生的损耗。

  （2） 木板可以沿着任意方向切割。

  （3） 木板可以任意摆放。

  （4） 用材不能重叠，不超过原材料的大小。

  （5） 原板材密度厚度均匀，形状为规则矩形。

  （6） 木板厚度和割缝宽度忽略不计。

问题分析：

  此问题为板材下料问题，只切割一种产品时，切割方案比较容易，对于切割多种产品时，需要尽可能的求解板材切割方案，确定不同的方案使得木板得到更多的利用。

  对于问题 1，求解出只切割 P1 产品的木板利用率最高的切割方案，若想木板利用率最高，只需切割产品的总面积最大，即在只切割同一种产品的情况下，只需切割产品的数量最多，问题可以转化为：经过对木板切割，使得获得的 P1 产品数量最多，建立线性规划模型，结合 MATLAB 里的 fmincon 函数求解。

  对于问题 2，求解出在一块木板上切割 P1 和 P3 产品，木板利用率由高到低排序前 3 的切割方案，对问题进行分析，可以将此问题转化为：在 P1 和 P3 产品个数可以为 0 的情况下，在木板上切割 P1 和 P3 产品，可将问题转化为两种产品的总面积之和最大的问题。同问题 1 一样，用线性规划模型，结合 MATLAB 里的 fmincon函数求解。

  对于问题 3，要求出木板总利用率最高的切割方案，经过对问题 3 的分析，可将问题转化为所需木板数量最少的问题，即两种木板的总面积除以所需木板的总面积最大。同问题 1、2 一样，用线性规划建立模型，结合 MATLAB 里的 fmincon 函数求解。

  对于问题 4，在完成 P1，P2，P3，P4 产品的生产任务的条件下，找出木板总利用率最高的切割方案。通过建立相关模型，我们首先找出利用率较高的 12 种切割方案，再建立线性规划模型对这 12 种切割方案进行优化组合，通过 LINGO 函数进行求解。

  对于问题 5，在给定 100 张 S1 木板，不考虑产品 P1，P2，P3，P4 的需求数量的条件下，找出总利润最大切割方案，经过对问题 5 的分析，可以将其转化为找出单张木板的切割利润最大的问题。类似问题 4，建立线性规划模型，通过 LINGO 函数进行求解。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：(代码和文档not free)

clc,clear
x1=0;
x2=0; 
n2=0; 
n=0;
for n1=0:8              % 长为3000的边全部放 横放 最多放 8  块
%     n2=0;             % 若将 n2 定义成局部变量 后面的 n2 清零操作可以不需要，因为每次循环结束 局部变量的值自动释放
    while n2*201+n1*3733000 
        n2=n2-1;        % 最后一次循环n2的值使 n2*201+n1*373>3000  超出 边界30 ，所以 n2 需要减 1
    end
    n=n2*4+n1*7;    % 竖放 最多放 4 行， 横放 最多放 7 行
    q=((n2*4+n1*7)*(373*201))/(3000*1500);
    fprintf('竖放%2d 列，横放%2d 列,总数%d,利用率%f\n',n2,n1,n,q); 
%     n=0;        % 清零 进行下次循环   重新计算下次循环总数
    n2=0;       % 清零 进行下次循环   为 "竖放" 计数
end

clc;clear; x=3000; y=1500;
x1=0; 
x2=0; 
i=0;
%同行不同列
fprintf('横放\n');
fprintf('（1）同行不同列\n');
for x1=1:7
    while x1*373+x2*4063000 
        x2=x2-1;
    end
    m1=x1*7;    % P1 最多放 7 行  15/2.01=7.4627
    m2=x2*6;    % P3 最多放 6 行  15/2.29=6.5502
    q=((m1*373*201)+(m2*406*229))/(3000*1500);
    fprintf('P1:%2d 列 ,	P1:%2d 个 ,	P3:%2d 列 ,	P3:%2d 个 ， 利 用率%f\n',x1,m1,x2,m2,q);
    x2=0;
end
 
%同列不同行
y2=0;
fprintf('（2）同列不同行\n'); 
for y1=1:7
    while 201*y1+229*y21500 
        y2=y2-1;
    end
    m1=y1*8; 
    m2=y2*7;
    q=((m1*373*201)+(m2*406*229))/(3000*1500);
    fprintf('P1:%2d 行 ,	P1:%2d 个 ,	P3:%2d 行 ,	P3:%2d 个 ， 利 用率%f\n',y1,m1,y2,m2,q);
    y2=0;
end
fprintf('竖放\n');
fprintf('（3）同行不同列\n'); 
x2=0;
for x1=1:14
    while x1*201+x2*2293000 
        x2=x2-1;
    end
    m1=x1*4; 
    m2=x2*3;
    q=((m1*373*201)+(m2*406*229))/(3000*1500);
    fprintf('P1:%2d 列 ,	P1:%2d 个 ,	P3:%2d 列 ,	P3:%2d 个 ， 利 用率%f\n',x1,m1,x2,m2,q);
    x2=0;
end
fprintf('（4）同列不同行\n'); 
y2=0;
for y1=1:3
    while y1*373+y2*4061500
        y2=y2-1;
    end
    m1=y1*14; 
    m2=y2*13;
    q=((m1*373*201)+(m2*406*229))/(3000*1500);
    fprintf('P1:%2d 行 ,	P1:%2d 个 ,	P3:%2d 行 ,	P3:%2d 个 ， 利 用率%f\n',y1,m1,y2,m2,q);
    y2=0;
end
%交叉
fprintf('（5）p1 竖放，p3 横放\n');
fprintf('同行不同列\n'); 
x2=0;
y2=0;
for x1=1:13
    while x1*201+x2*4063000 
        x2=x2-1;
    end
    m1=x1*4; 
    m2=x2*6;
    q=((m1*373*201)+(m2*406*229))/(3000*1500);
    fprintf('P1:%2d 列 ,	P1:%2d 个 ,	P3:%2d 列 ,	P3:%2d 个 ， 利 用率%f\n',x1,m1,x2,m2,q);
    x2=0;
end
y2=0;
fprintf('（6）p1 竖放，p3 横放,不同行\n'); 
for y1=1:4
    while y1*373+y2*2291500 
        y2=y2-1;
    end
    m1=y1*14; 
    m2=y2*7;
    q=((m1*373*201)+(m2*406*229))/(3000*1500);
    fprintf('P1:%2d 列 ,	P1:%2d 个 ,	P3:%2d 列 ,	P3:%2d 个 ， 利 用率%f\n',y1,m1,y2,m2,q);
    x2=0;
end
 
fprintf('（7）p1 横放，p3 竖放，同行\n'); 
for x1=1:7
    while x1*373+x2*2293000 
        x2=x2-1;
    end
    m1=x1*7; 
    m2=x2*3;
    q=((m1*373*201)+(m2*406*229))/(3000*1500);
    fprintf('P1:%2d 列 ,	P1:%2d 个 ,	P3:%2d 列 ,	P3:%2d 个 ， 利 用率%f\n',x1,m1,x2,m2,q);
    x2=0;
end
y2=0;
fprintf('（8）p1 横放，p3 竖放，不同行\n'); 
for y1=1:5
    while y1*201+y2*4061500 
        y2=y2-1;
    end
    m1=y1*8; 
    m2=y2*13;
    q=((m1*373*201)+(m2*406*229))/(3000*1500);
    fprintf('P1:%2d 列 ,	P1:%2d 个 ,	P3:%2d 列 ,	P3:%2d 个 ， 利 用率%f\n',y1,m1,y2,m2,q);
    x2=0;
end

clc;clear; 
x=3000; 
y=1500;
x1=0; 
x2=0; 
i=0; 
s=0;
qq=0;
%同行不同列
 
fprintf('横放\n');
fprintf('（1）同行不同列\n'); 
for x1=1:6
    while x1*373+x2*4063000 
        x2=x2-1;
    end
    m1=x1*7; 
    m2=x2*6;
    q=((m1*373*201)+(m2*406*229))/(3000*1500);
    fprintf('P1:%2d 列 ,	P1:%2d 个 ,	P3:%2d 列 ,	P3:%2d 个 ， 利 用率%f',x1,m1,x2,m2,q);
    while s*m1