线性矩阵不等式（LMI）（一）：简单介绍

线性矩阵不等式（LMI）（一）：简单介绍

主要从以下三个方面介绍：

1. 什么是线性矩阵不等式(LMI)
2. 为什么要用线性矩阵不等式(LMI)
3. 线性矩阵不等式的发展（控制系统中）

文章目录

• • 线性矩阵不等式（LMI）（一）：简单介绍
  • • 1. 线性矩阵不等式
    • • 1.1 一般形式
      • 1.2 标准形式
      • 1.3 二者关系
      • 2. 线性矩阵不等式的优点
      • • 2.1 LMI 是一个凸集
        • 3. 线性矩阵不等式的发展
        • • 参考文献

            1. 线性矩阵不等式

            如名字所示线性矩阵不等式三要素为：

            • 线性 - 注意双线性时，LMI不好求解(非凸问题)；例：在不等式中出现 P A K PAK PAK形式，其中 P , K P,K P,K都为未知变量；可以利用消元法/换元法[1]转化为LMI形式；
            • 矩阵变量 - 可以表示成一般形式/标准形式；
            • 不等号 - 表示矩阵的正定/负定，而不是大小关系；

              1.1 一般形式

              • LMI的一般形式可以表示为[2]：

                L ( X ) = D T X + X T D + ∑ i = 1 l ( E i T X F i + F i T X T E i ) + Q 0(x2​−5 ​x1​+25 ​−1​)(x2​+5 ​x1​−25 ​+1​)>0.​

                根据上式可得 ( x 1 , x 2 ) (x_1,x_2) (x1​,x2​)取值范围为，下图所示公共部分。

                

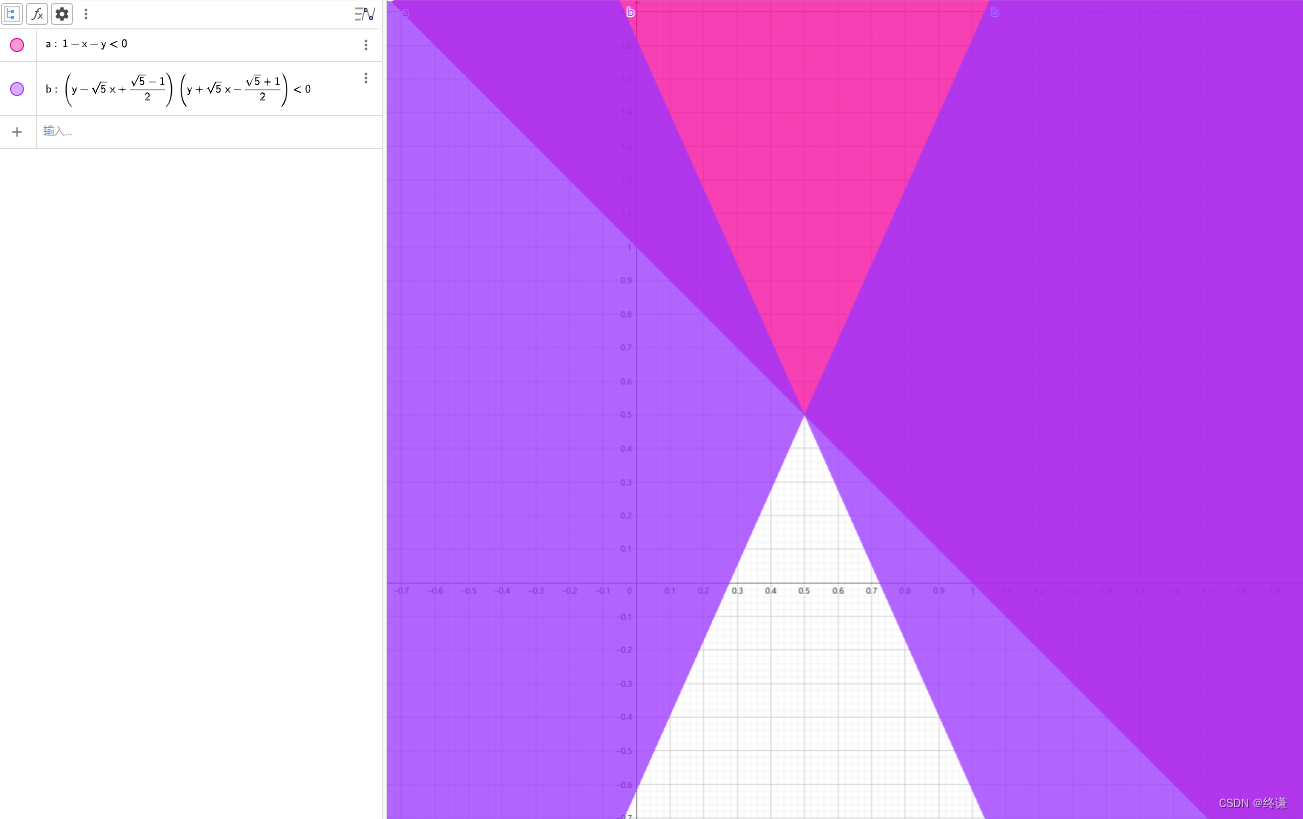
                1.3 二者关系

                • 让标准形式中 A i , i = 1 , . . . , n A_i,i=1,...,n Ai​,i=1,...,n 为一般形式中 P P P的基底，则 P P P可表示为 P = A 0 + x 1 A 1 + ⋅ ⋅ ⋅ + x n A n P = A_0 + x_1A_1 + \cdot\cdot\cdot+x_nA_n P=A0​+x1​A1​+⋅⋅⋅+xn​An​。定义 T i = A T A i + A i T A ， T_i = A^TA_i+A_i^TA， Ti​=ATAi​+AiT​A，带入到标准形式中，则可将一般形式转化为标准形式

                  L ( P ) = T 0 + ∑ i = 1 n x i T i L(P) = T_0+\sum_{i=1}^nx_iT_i L(P)=T0​+i=1∑n​xi​Ti​

                  • 例：根据Lyapunov稳定理论，二维线性系统

                    x ˙ ( t ) = A x ( t ) , x ( 0 ) ≠ 0 \dot x(t) = A x(t) , x(0)\neq 0 x˙(t)=Ax(t),x(0)=0

                    稳定的充要条件是，存在满足不等式

                    A T P + P A