
置换多元方差分析(Permutational multivariate analysis of variance,PERMANOVA),又称非参数多因素方差分析(nonparametric multivariate analysis of variance)、或者ADONIS分析。它利用距离矩阵(如欧式距离、Bray-Curtis距离)对总方差进行分解,分析不同分组因素或不同环境因子对样品差异的解释度,并使用「置换检验」对各个变量解释的统计学意义进行显著性分析。
一个例子
比如,对宏基因组检测的物种丰度数据进行PCA/NMDS/PCoA降维可视化后,不同组的样品之间存在一些重叠,那怎么判断这些组之间的样品构成是否存在显著差别呢?这就需要用到PERMANOVA检验了,检验不同组的样品中心点是否重叠。
 example
example

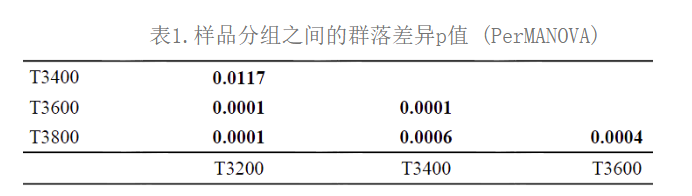
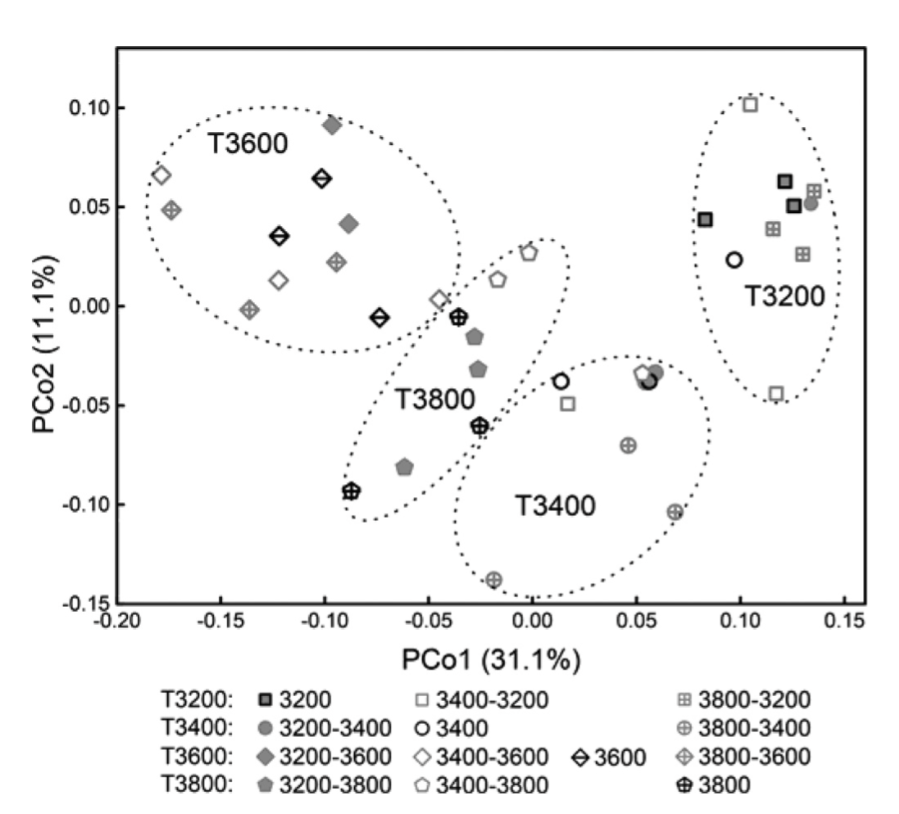
以上面的PCoA图为例,椭圆圈出的四组样品点正好对应四个海拔分组,这四组样品之间的群落差异是否显著呢?检验组间群落差异本质上是检验距离矩阵之间的差异,普通的ANOVA分析无能为力。而基于距离矩阵的PerMANOVA分析则表明,这四个分组两两之间差异是显著的(p









