主观Bayes方法是解决标准Bayes公式所存在的需要由逆概率去求原概率的问题。
全概率公式如下:
设时间A1,A2,A3,…,An满足:
(1)任意两个事件都不相容,即当i≠j时,有Ai∩Aj=Φ(i=1,2,….,n;j=1,2,…,n)
(2)P(Ai)>;0(i=1,2,…,n)
(3)样本空间D,对任何事件B有下式成立:
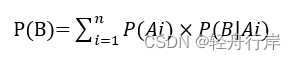
Bayes公式:
设事件A1,A2,…,An满足上面的条件,则对任何事物B有下式成立:
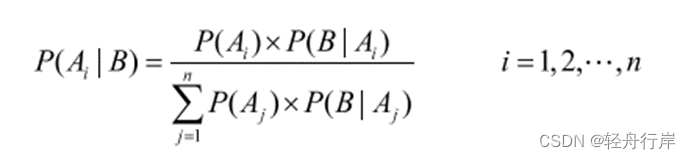
该定理称为Bayes定理,上式也称为Bayes公式。
将全概率公式代入Bayes公式,有:
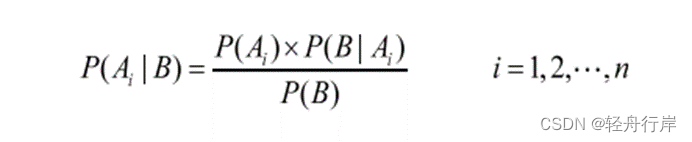
表示形式,在主观Bayes方法中,知识是用产生式表示的,形式为:
IF E THEN (LS,LN) H
其中,(LS,LN)表示该知识的知识强度,LS为充分性度量,LN为必要性度量。
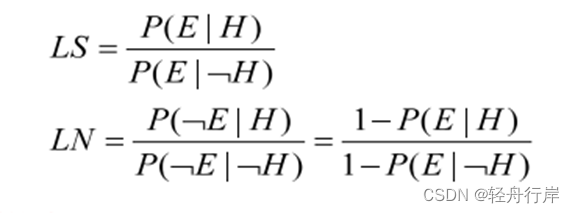
几率函数:
X的几率等于X出现的概率与X不出现的概率之比,且P(X)与O(X)的变化一致。
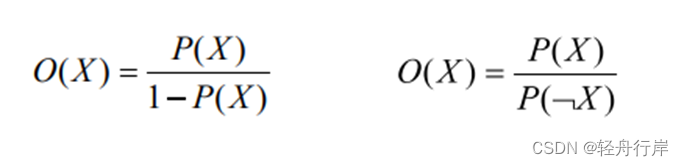
当E为真时,可以用LS将H的先验几率O(H)更新为其后验几率O(H|E)
当E为假时,可以用LN将H的先验几率O(H)更新为其后验几率O(H|﹁E)
LS与LN的关系
由于E和﹁E不会同时支持或同时排斥H,因此只有下面三种情况存在:
a) LS>1且LN









