斐波那契数列的C语言多种实现方法（递归、循环、动态规划、矩阵乘法和公式法）

介绍

斐波那契数列是一个非常有趣的数列，它的每一项都是前两项的和，前两项分别为0和1。这个数列的前几项是：0、1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987、1597、2584、4181、6765。这个数列的公式可以表示为：

• F0 = 0
• F1 = 1
• Fn = Fn-1 + Fn-2（n >= 2）

  这个数列有许多有趣的性质，例如，两个连续的斐波那契数之比会收敛于黄金比例，约等于1.61803399。

  在这篇博客中，我们将探讨如何使用C语言实现斐波那契数列，并讨论各种方法的时间复杂度。

  
  （图片来源网络，侵删）

  递归实现

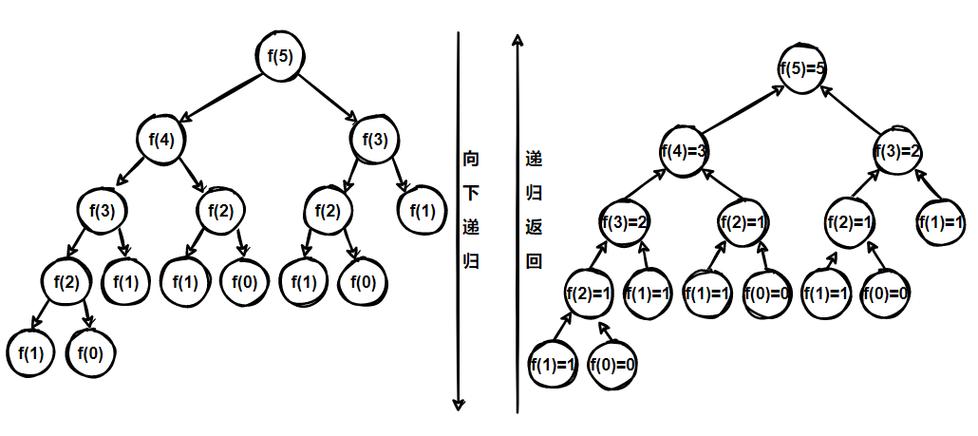
  递归是最直观的方法，直接根据斐波那契数列的定义F(n) = F(n-1) + F(n-2)来实现。但是这种方法的时间复杂度是O(2^n)，因为它会重复计算很多项，效率非常低。

  #include
  // 斐波那契数列函数
  int fibonacci(int n) {
      if(n == 0) {
          return 0;
      } else if(n == 1) {
          return 1;
      } else {
          return fibonacci(n-1) + fibonacci(n-2);
      }
  }
  int main() {
      int n;
      printf("请输入一个整数：");
      scanf("%d", &n);
      printf("斐波那契数列的第%d项为：%d\n", n, fibonacci(n));
      return 0;
  }
  

  循环实现

  循环实现是一种更有效的方法，它使用两个变量来保存前两项，然后通过循环来计算第n项。这种方法的时间复杂度是O(n)，效率比递归高很多。

  #include
  // 斐波那契数列函数
  int fibonacci(int n) {
      if(n {1,1},{1,0}};
      if (n == 0)
          return 0;
      power(F, n - 1);
      return F[0][0];
  }
  void multiply(int F[2][2], int M[2][2]) {
      int x =  F[0][0]*M[0][0] + F[0][1]*M[1][0];
      int y =  F[0][0]*M[0][1] + F[0][1]*M[1][1];
      int z =  F[1][0]*M[0][0] + F[1][1]*M[1][0];
      int w =  F[1][0]*M[0][1] + F[1][1]*M[1][1];
    
      F[0][0] = x;
      F[0][1] = y;
      F[1][0] = z;
      F[1][1] = w;
  }
  void power(int F[2][2], int n) {
      int i;
      int M[2][2] = {{1,1},{1,0}};
    
      // n - 1 times multiply the matrix to {{1,0},{0,1}}
      for (i = 2; i