因素分解理论:
1919年统计学家沃伦·珀森斯(Warren Persons)在他的论文《商业环境的指标》中首次提出了确定性因素分解(time series decomposition)思想。之后,该方法广泛应用于宏观经济领域时间序列的分析和预测。
珀森斯认为尽管不同的经济变量波动特征千变万化,因果关系的影响错综复杂,但所有的序列波动都可以归纳为受到如下四个因素的综合影响:
(1)长期趋势(trend)。序列呈现出明显的长期递增或递减的变化规律。
(2)循环波动(circle)。序列呈现出从低到高,再从高到低的反复循环波动。循环周期可长可短,不一定是固定的。循环波动通常在经济学中作为经济景气周期指标。
(3)季节性变化(season)。序列呈现出和季节变化相关的稳定周期性波动,后来季节性变化的周期拓展到任意稳定周期。
(4)随机波动(irrelevance)。除了长期趋势、循环波动和季节性变化之外,其他不能用确定性因素解释的序列波动都属于随机波动。
统计学家假定序列会受到这四个因素中的全部或部分的影响,从而呈现出不同的波动特征。换言之,任何一个时间序列都可以用这四个因素的某个函数进行拟合: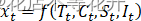 。
。
最常用的两个函数是加法函数和乘法函数,相应的因素分解模型称为加法模型和乘法模型。
加法模型: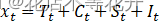
乘法模型: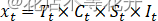
ARIMA模型也可以对具有季节效应的序列建模。根据季节效应提取的方式不同,又 底分为ARIMA加法模型和ARIMA乘法模型。
ARIMA加法模型是指定列中季节效应和其他效应之间是加法关系,即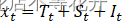
这时,各种效应信息的提取都非常容易。通常简单的周期步长差分即可将序列中的季节信息提取充分,简单的低阶差分即可将趋势信息提取充分,提取完季节信息和趋势信息之后的残差序列就是一个平稳序列,可以用ARMA模型拟合。
但更为常见的情况是,序列的季节效应、长期趋势效 应和随机波动之间存在复杂的交互影响关系,简单的季节加法模型并不足以充分提取其中的相关关系,这时通常需要采用季节乘法模型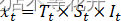
例题:某城市1980年1月至1995年8月每月屠宰生猪数量如下表所示(行数据)。
(1)绘制时序图,直观考察该序列的确定性因素特征。
(2)选择适当的模型对该序列进行因素分解。
(3)选择适当的模型对该序列进行为期5年的预测。
分析思路如下:
1、导入数据并生成时间序列
m









