数学建模--（3.1）相关系数

目录

相关系数

皮尔逊相关系数

1.总体皮尔逊相关系数

2.样本皮尔逊相关系数​编辑

3.相关理解

4. 矩阵散点图

5.皮尔逊相关系数计算

6.使用EXCEL美化相关系数表

7.对皮尔逊相关系数进行假设检验

8.计算相关系数和p值

9.皮尔逊检验的条件

斯皮尔曼spearman相关系数

1.第一定义

2.第二定义

3.斯皮尔曼相关系数的假设检验

 两个相关系数的选择

相关系数

        两种最为常用的相关系数：皮尔逊pearson相关系数和斯皮尔曼spearman等级相关系数。它们可用来衡量两个变量之间的相关性的大小，根据数据满足的不同条件，我们要选择不同的相关系数进行计算和分析（建模论文中最容易用错的方法）。

皮尔逊相关系数

1.总体皮尔逊相关系数

假设有两个变量X、Y，那么两变量间的皮尔逊相关系数可通过以下公式计算：

 皮尔逊相关系数也可以看成是剔除了两个变量量纲影响，即将X和Y标准化后的协方差。

2.样本皮尔逊相关系数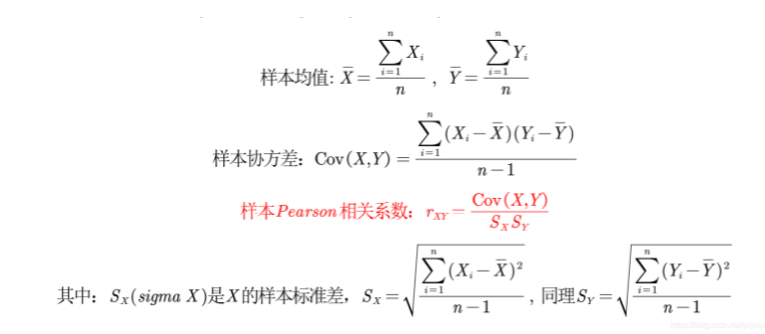

3.相关理解

1. 这里的相关系数只是用来衡量两个变量线性相关程度的指标；也就是说，你必须先确认这两个变量是线性相关的，然后这个相关系数才能告诉你他俩相关程度如何。
2. 
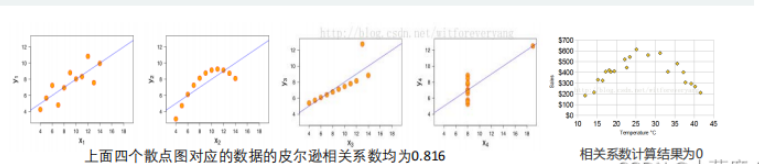
3.  非线性相关也会导致线性相关系数很大，例如图2。
4. 离群点对相关系数的影响很大，例如图3，去掉离群点后，相关系数为0.98。
5. 如果两个变量的相关系数很大也不能说明两者相关，例如图4，可能是受到了异常值的影响。
6. 相关系数计算结果为0，只能说不是线性相关，但说不定会有更复杂的相关关系（非线性相关），例如图5。

        如果两个变量本身就是线性的关系，那么皮尔逊相关系数绝对值大的就是相关性强，小的就是相关性弱；

        在不确定两个变量是什么关系的情况下，即使算出皮尔逊相关系数，发现很大，也不能说明那两个变量线性相关，甚至不能说他们相关，我们一定要画出散点图来看才行。

4. 矩阵散点图

在计算皮尔逊相关系数之前,一定要做出散点图来看两组变量之间是否有线性关系

使用Spss : 图形 ‐ 旧对话框 ‐ 散点图/点图 ‐ 矩阵散点图

5.皮尔逊相关系数计算

使用corrcoef函数(correlation coefficient相关系数)

R = corrcoef(A)
R = corrcoef(A,B)

返回 A 的相关系数的矩阵，其中 A 的列表示随机变量（指标），行表示观测值（样本）。

返回两个随机变量 A 和 B （两个向量）之间的系数。

6.使用EXCEL美化相关系数表

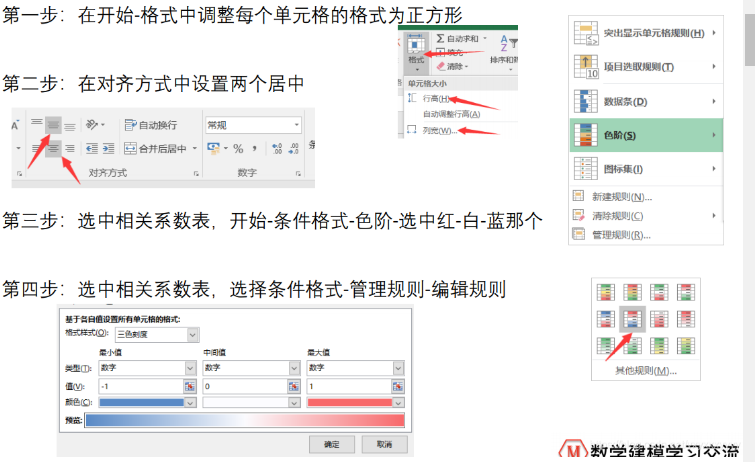
7.对皮尔逊相关系数进行假设检验

方法一：

1. 
2. 在原假设条件成立的情况下，利用被检测的量构造出一个符合某一分布的统计量
3. 将检验的值代入统计量中，得到特定的值（检验值t^*）
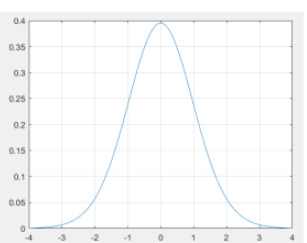
4. 根据统计量的分布情况，绘制该分布的概率密度函数 pdf，并给定一个置信水平，根据置信水平查表寻找临界值，画出检验统计量的接受域和拒绝域。
5. 判断t^*在拒绝域还是接受域

x = -4:0.1:4;
y = tpdf(x,28); %用于画t分布的pdf
plot(x,y,'-')
grid on % 在画出的图上加上网格线

方法二：p值判断法

得到检验值后根据这个值计算其对应的概率，再用1减去这个数得到p值

disp('该检验值对应的p值为：')
disp((1-tcdf(3.055,28))*2) %双侧检验的p值要乘以2，单侧的不用
%tcdf : 累积分布函数

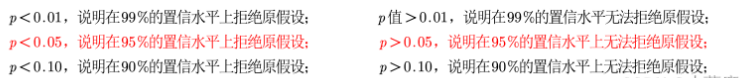
8.计算相关系数和p值

[R,P] = corrcoef(Test)

R返回的是相关系数表，P返回的是对应于每个相关系数的p值

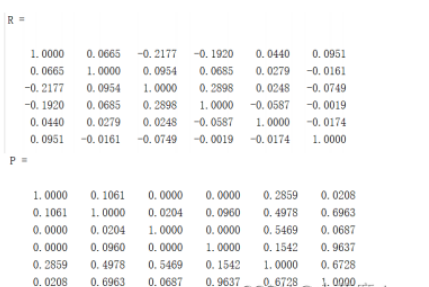
%% 计算各列之间的相关系数以及p值
[R,P] = corrcoef(Test)
% 在EXCEL表格中给数据右上角标上显著性符号
P  0.01) % 标记2颗星的位置
(P  0.05) % 标记1颗星的位置

 标注：

• 没有星星表示不显著
• *(一颗星星)表示在置信水平为90%时显著异于零，p值小于0.1
• **(两颗星星)表示在置信水平为95%时显著异于零，p值小于0.05
• ***(三颗星星)表示在置信水平为99%时显著异于零，p值小于0.01

  9.皮尔逊检验的条件

  1. 实验数据通常假设是成对的来自于正态分布的总体。（最重要）
  2. 实验数据之间的差距不能太大。皮尔逊相关性系数受异常值的影响比较大。
  3. 每组样本之间是独立抽样的。构造t统计量时需要用到。

  ---

  检验正态分布：

  雅克‐贝拉检验(Jarque‐Bera test)（大样本n>30）

  

   偏度和峰度：

  

   

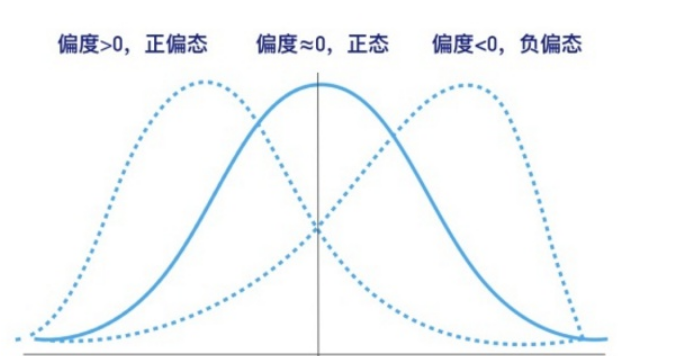
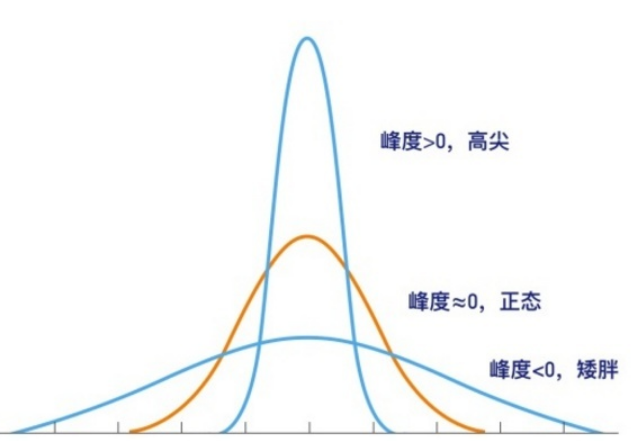
   偏度≈0时，可认为分布是对称的，服从正态分布，峰度=3

  

  matlab实现：

  MATLAB中进行JB检验的语法

  [h,p] = jbtest(x,alpha)

  • 当输出 h =1时，表示拒绝原假设(不是正态分布)，h=0则代表不能拒绝原假设(正态分布)。
  • p代表了 p值
  • alpha就是显著性水平，一般取0.05，此时置信水平为1‐0.05=0.95

    x就是我们要检验的随机变量，注意这里的x只能是向量。

    %% 正态分布检验
    % 检验第一列数据是否为正态分布
    [h,p] = jbtest(Test(:,1),0.05)
    % 用循环检验所有列的数据
    n_c = size(Test,2);  %数据的列数
    H = zeros(1,6); %初始化两个数组 一列六行
    P = zeros(1,6);
    for i = 1:n_c
    	[h,p] = jbtest(Test(:,i),0.05);
    	H(i)=h;
    	P(i)=p;
    end
    disp(H)
    disp(P)
    

    ---

    Shapiro-wilk检验(小样本：3