神经网络系列---激活函数

文章目录

• • 激活函数
  • • Sigmoid 激活函数
    • Tanh激活函数
    • ReLU激活函数
    • Leaky ReLU激活函数
    • Parametric ReLU激活函数 （自适应Leaky ReLU激活函数）
    • ELU激活函数
    • SeLU激活函数
    • Softmax 激活函数
    • Swish 激活函数
    • Maxout激活函数
    • Softplus激活函数

      ---

      激活函数

      

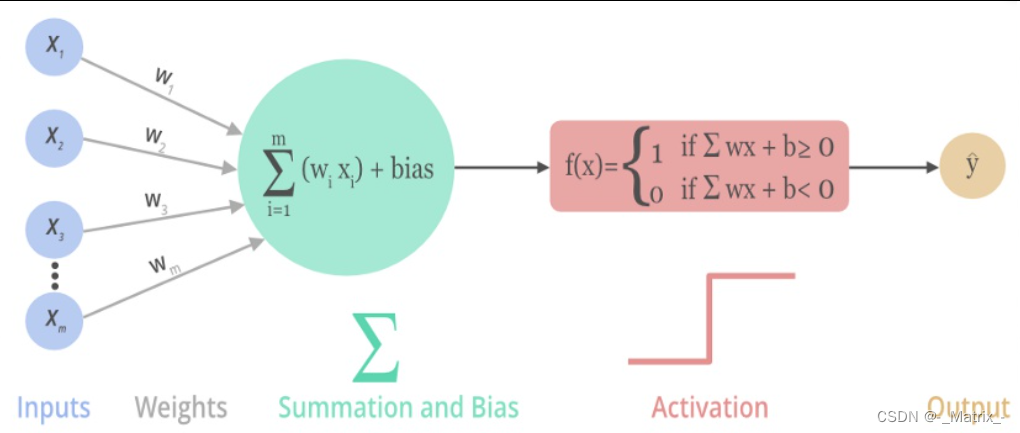
      一般来说，在神经元中，激活函数是很重要的一部分，为了增强网络的表示能力和学习能力，神经网络的激活函数都是非线性的，通常具有以下几点性质：

      • 连续并可导（允许少数点上不可导），可导的激活函数可以直接利用数值优化的方法来学习网络参数；
      • 激活函数及其导数要尽可能简单一些，太复杂不利于提高网络计算率；
      • 激活函数的导函数值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效率和稳定性。

        Sigmoid 激活函数

        Sigmoid函数，也称为Logistic函数，是一种常用的激活函数之一。它将输入值映射到一个介于0和1之间的连续输出值。

        Sigmoid函数的数学表达式为：

        数学推导：
        对Sigmoid函数f(x) = 1 / (1 + exp(-x))，我们可以通过链式法则对其求导。
        首先，我们计算Sigmoid函数的导数f'(x)：
        f'(x) = d/dx(1 / (1 + exp(-x)))
        接下来，我们将求导式进行变形，以便更方便地计算：
        f'(x) = 1 / (1 + exp(-x))^2 * exp(-x)
        因此，Sigmoid函数的导数f'(x)的表达式为：
        f'(x) = f(x) * (1 - f(x))
        这个表达式可以用于计算任意输入x处的Sigmoid函数的导数。
        

        

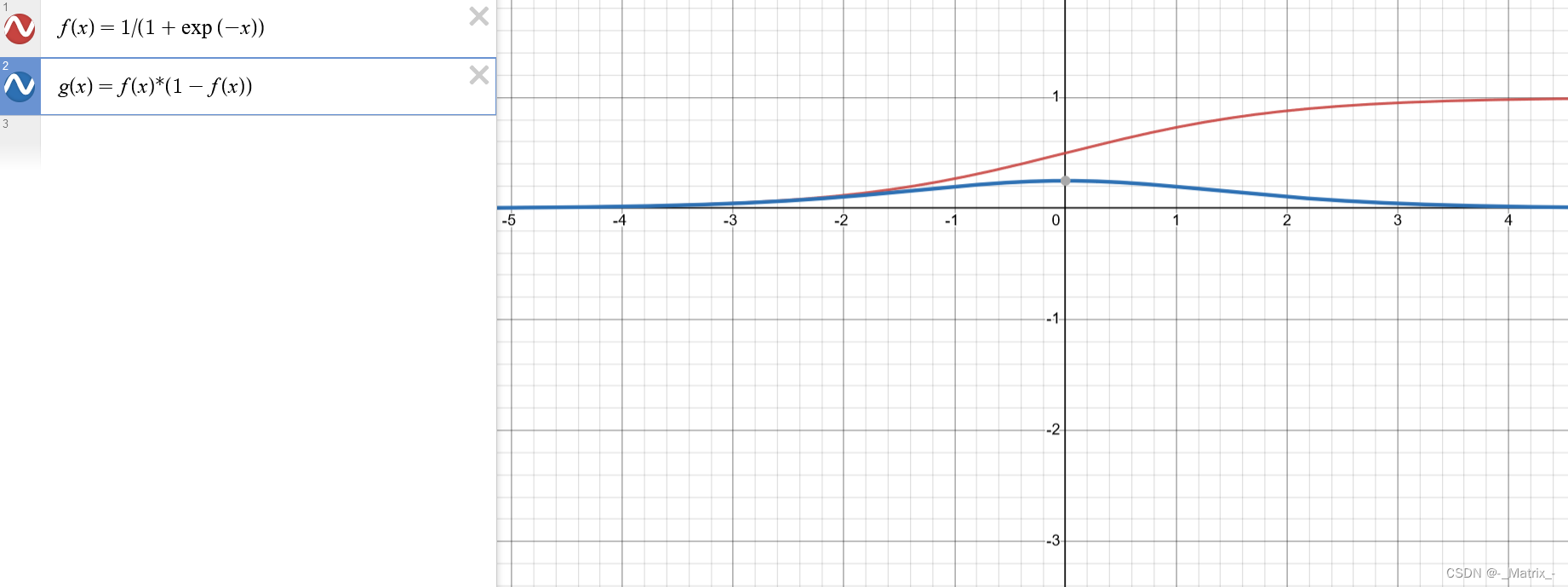
        C++实现Sigmoid函数的示例代码：

        #include 
        // Sigmoid函数的实现
        double sigmoid(double x) {
            return 1.0 / (1.0 + exp(-x));
        }
        // Sigmoid函数的导数实现
        double sigmoidDerivative(double x) {
            double fx = sigmoid(x);
            return fx * (1.0 - fx);
        }
        int main() {
            double x = 2.0; // 示例输入值
            // 调用Sigmoid函数计算输出
            double result = sigmoid(x);
            // 调用Sigmoid函数的导数计算输出
            double derivative = sigmoidDerivative(x);
            // 输出结果
            printf("Sigmoid(%f) = %f\n", x, result);
            printf("Sigmoid的导数(%f) = %f\n", x, derivative);
            return 0;
        }
        

        其中，exp表示自然常数e（约等于2.71828）的指数函数。

        Sigmoid函数的特点是在输入值较大或较小时，输出接近于1或0，而在输入值接近0时，输出接近于0.5。这种S型曲线形状使得Sigmoid函数在二分类问题中常被用作输出层的激活函数，将输出解释为概率值，表示正类的概率。

        Sigmoid函数具有以下优点和缺点：

        优点：

        1. 可以将输入映射到介于0和1之间的概率值，适用于二分类问题中将输出解释为概率的情况。
        2. Sigmoid函数在输入接近0时，输出接近于0.5，具有平滑的、连续的特性。
        3. Sigmoid函数具有可导性，这对于使用梯度下降等基于梯度的优化算法进行模型训练是重要的。

        缺点：

        1. Sigmoid函数在输入较大或较小的情况下，输出接近于0或1，导致梯度饱和，使得反向传播时梯度变得非常小，造成梯度消失的问题。这限制了Sigmoid函数在深度神经网络中的应用。
        2. Sigmoid函数的指数计算较为复杂，相比于其他激活函数，计算代价较高。
        3. Sigmoid函数输出的值不是以0为中心的，即其输出均值不为0，这可能导致网络在训练过程中的收敛速度变慢。

        综上所述，尽管Sigmoid函数在过去被广泛应用于神经网络中，但随着深度学习的发展，人们更倾向于使用其他激活函数，如ReLU及其变种，因为它们能够缓解梯度消失问题并提供更好的性能。然而，在某些特定情况下，Sigmoid函数仍然可以有所用处，例如需要将输出解释为概率的二分类问题。

        Tanh激活函数

        Tanh函数（双曲正切函数）是一种常用的激活函数，它将输入值映射到一个介于-1和1之间的连续输出值。

        Tanh函数的数学表达式为：

        数学推导：
        Tanh函数的数学表达式为：
        f(x) = (exp(x) - exp(-x)) / (exp(x) + exp(-x))
        我们可以通过对Tanh函数进行求导，得到其导数的数学表达式。
        首先，我们令y = Tanh(x)，则Tanh函数可以表示为：
        y = (exp(x) - exp(-x)) / (exp(x) + exp(-x))
        对y求导，即计算dy/dx。
        使用除法的求导法则和指数函数的求导法则，我们可以得到：
        dy/dx = [(exp(x) + exp(-x))(exp(x) + exp(-x)) - (exp(x) - exp(-x))(exp(x) - exp(-x))] / (exp(x) + exp(-x))^2
        化简上述表达式，我们可以得到Tanh函数的导数的数学表达式：
        dy/dx = 1 - (Tanh(x))^2
        因此，Tanh函数的导数为 1 减去其本身的平方。
        

        

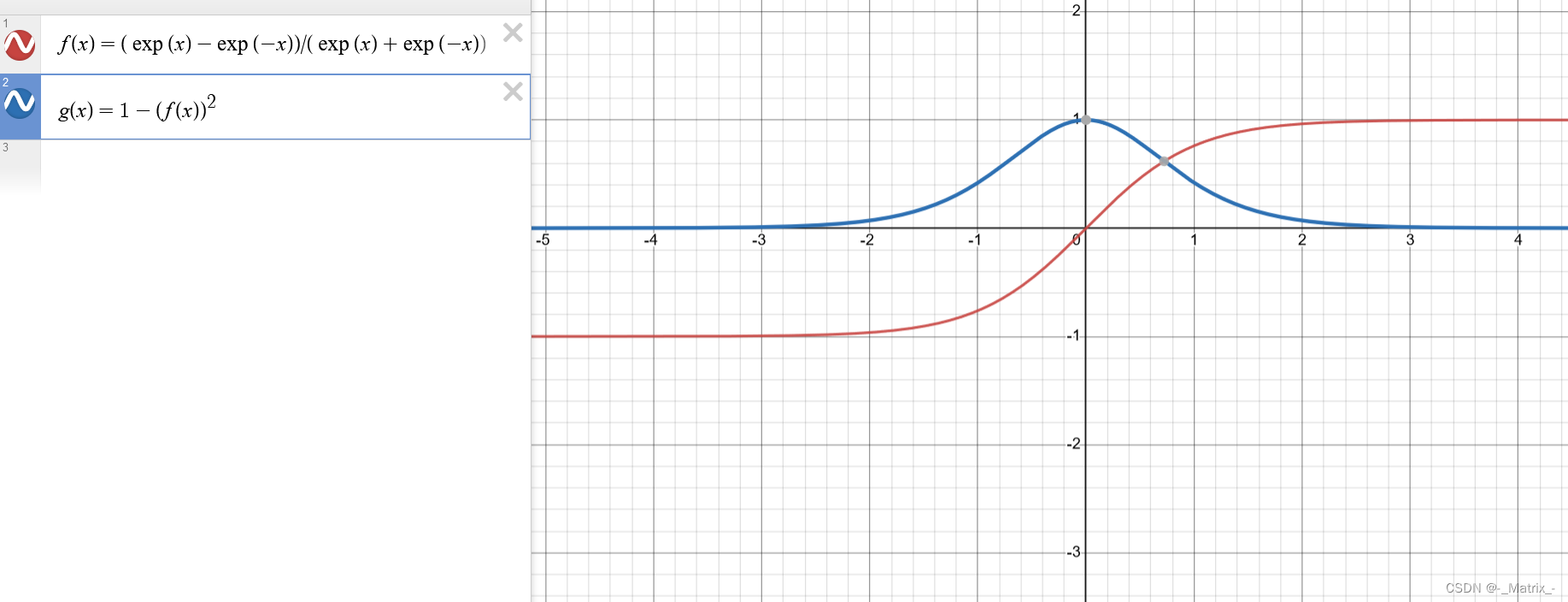
        Tanh函数可以看作是Sigmoid函数的变种，它具有Sigmoid函数的S型曲线形状，但输出范围更广，从-1到1。

        Tanh函数的特点包括：

        1. 在输入接近0时，输出接近于0，具有零中心化的特性。
        2. Tanh函数的输出在输入为负时接近于-1，在输入为正时接近于1。
        3. Tanh函数是可导的，对于使用梯度下降等基于梯度的优化算法进行模型训练是可行的。

        以下是使用C++实现Tanh函数的示例代码：

        #include 
        // Tanh函数的实现
        double tanh(double x) {
            return (exp(x) - exp(-x)) / (exp(x) + exp(-x));
        }
        // Tanh函数的导数实现
        double tanh_derivative(double x) {
            double tanh_x = tanh(x);
            return 1 - tanh_x * tanh_x;
        }
        int main() {
            double x = 2.0; // 示例输入值
            // 调用Tanh函数计算输出
            double result = tanh(x);
            // 调用Tanh函数的导数计算输出
            double derivative = tanh_derivative(x);
            // 输出结果
            printf("Tanh(%f) = %f\n", x, result);
            printf("Tanh Derivative(%f) = %f\n", x, derivative);
            return 0;
        }
        

        Tanh函数（双曲正切函数）具有以下优点和缺点：

        优点：

        1. Tanh函数的输出范围是介于-1和1之间，相比于Sigmoid函数，Tanh函数的输出具有零中心化的特性，使得数据在处理时更接近原点。
        2. Tanh函数在输入接近0时，输出接近于0，可以将数据映射到更接近原点的区域，有助于模型的收敛。
        3. Tanh函数是可导的，对于使用梯度下降等基于梯度的优化算法进行模型训练是可行的。

        缺点：

        1. Tanh函数在输入较大或较小的情况下，输出接近于1或-1，导致梯度饱和，使得反向传播时梯度变得非常小，造成梯度消失的问题，尤其在深度神经网络中。
        2. Tanh函数的指数计算较为复杂，相比于其他激活函数，计算代价较高。
        3. Tanh函数的输出值域为[-1, 1]，这使得它对于某些任务而言，可能不是最优的激活函数选择。

        综上所述，尽管Tanh函数具有一些优点，但在深度神经网络中，它容易出现梯度消失的问题，因此在实践中，ReLU及其变种等激活函数更常用。然而，Tanh函数仍然可以在特定情况下使用，例如需要将输出值范围控制在[-1, 1]之间的任务，或者在某些循环神经网络（RNN）的隐藏层中使用。

        ReLU激活函数

        ReLU（Rectified Linear Unit）函数是一种常用的激活函数，它在深度学习中广泛使用，特别是在卷积神经网络（CNN）中。

        ReLU函数的定义很简单：

        ReLU函数的数学表达式为：
        f(x) = max(0, x)
        ReLU函数在输入大于0时的导数为1，在输入小于等于0时的导数为0。
        数学推导如下：
        当 x > 0 时，ReLU函数为 f(x) = x。其导数为：
        f'(x) = 1
        当 x