【人工智能概论】变分自编码器（Variational Auto Encoder , VAE）

慈云数据 2024-03-13 技术支持 46 0

【人工智能概论】变分自编码器（Variational Auto Encoder , VAE）

文章目录

【人工智能概论】变分自编码器（Variational Auto Encoder , VAE）
一.回顾AE
二.VAE简介
三.VAE为什么好
- 1.AE有什么不好
- 2.VAE怎么解决AE的问题
- 3.有两个困难
- 4.意想不到的问题
- 5.现在的VAE能做到什么
- 6.VAE为什么好
- 四.VAE的公式推导
- 五.重新参数技巧（reparameterization trick）
- 六.代码实现
  一.回顾AE
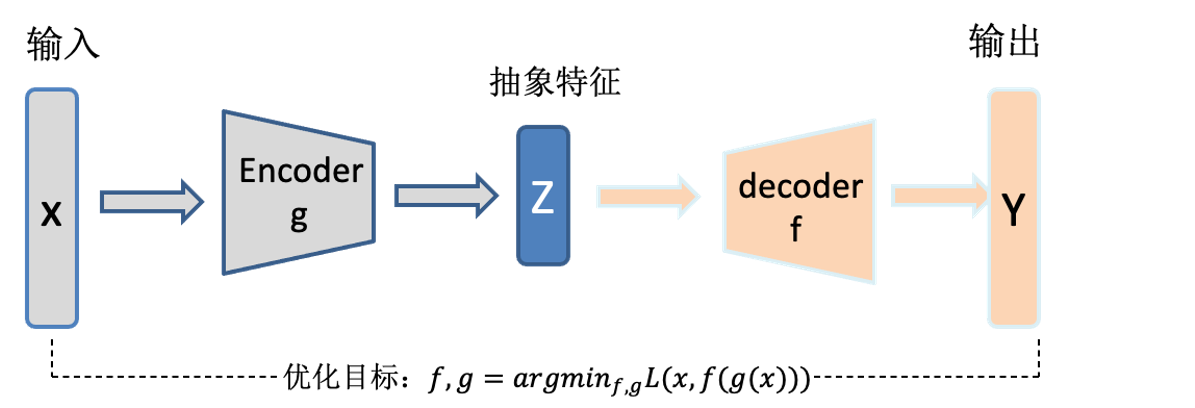
  - 更多的详见自编码器简介，尤其是AE的缺点。
    二.VAE简介
    - 变分自编码器（variational auto-encoder，VAE），常被用于生成数据，是常见的三种生成模型之一，它可以从训练数据中来建模真实的数据分布，然后再用学习到的模型和分布去生成、构建新的数据。
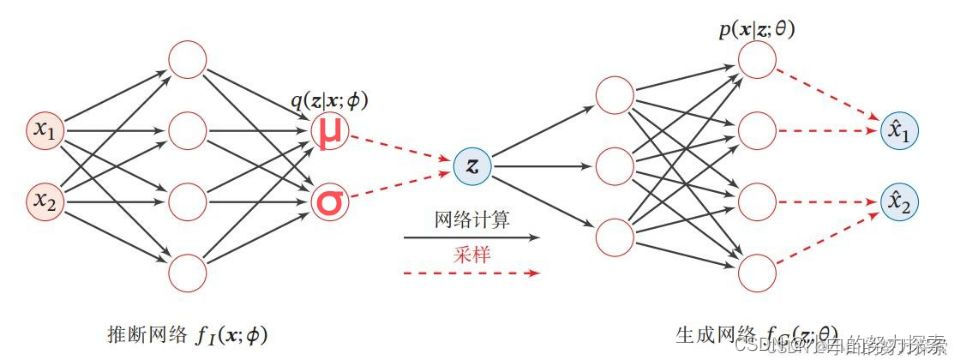
    - 其网络结构同AE类似，但其编码器并不是直接输出一个隐变量，而是输出一个多维高斯分布的均值( u )和方差( δ )，然后在所获得的分布中进行采样，得到一个 z，将z送入到解码器中进行解码，目标同AE类似，即将利用 z还为原始的输入。
    - 通过上述不难发现，VAE可以做到一个输入对应多个输出，并且这些输出之间尽可能类似，而AE的输入输出是一一对应的，因此值得注意的是VAE可以做为生成模型使用，而AE不能做生成模型，前者可以生成新的数据，而后者不能（这点在AE的缺点介绍中也有所提及）。
    - VAE网络架构
      
      - VAE的效果简视（无标签聚类，特征学习，过渡生成）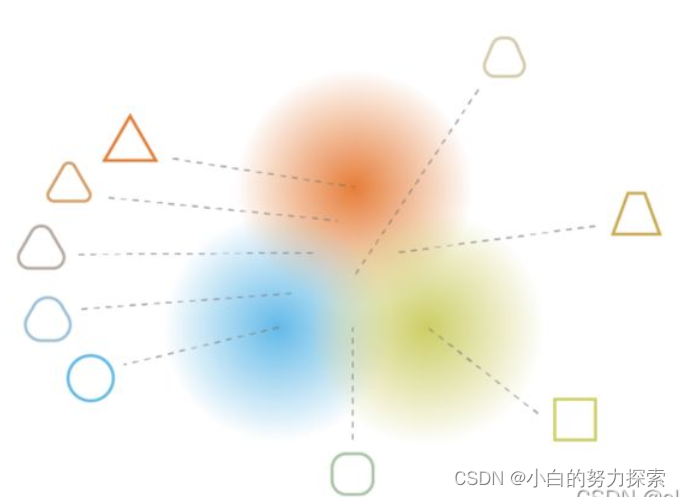
      
      三.VAE为什么好
      
      1.AE有什么不好
      - 映射空间不连续，无规则，无界。
      - 更多的详见自编码器简介
        2.VAE怎么解决AE的问题
        
        将每组数据编码为一个分布
        
        不是某一个点，而是分布区域内任取一点都要尽可能被还原的像原始数据。
        但这样有一个问题，不同数据对应的分布间势必会有重叠，重叠区域该怎么办，直觉告诉我们应该是让这部分数据跟谁都像点，但又不是很像。
        确实如此，那怎么做到那？在损失函数上下功夫，算损失函数要考虑整个分布中的点，对整个分布区域内的点的损失进行加权求和，具体来说，让越靠近均值点的部分还原出来的与原始数据越像，loss越小，且这部分数据占的权重要大一些，而越靠外的还原效果越差，但是还是要有点像的，loss就要大一点，且这部分数据占的权重要小一点，总体上还是希望损失越小越好的，这样就迫使重叠区域内的点“左右逢源”使得损失处于一个相对较低的情况。
        这样操作下来，既解决了映射空间不连续（用分布代替唯一编码），也解决了编码缺少语义的问题（重叠区域“左右逢源”），无界问题也得到缓解（数据点相对更集中）。
        这样得到的编码理论上讲，具有语义，且存在语义过渡。
        3.有两个困难
        
        如何让一个输入数据对应一个分布？
        在code上下手，可让编码器的输出为一个多维高斯分布的均值( u )和方差( δ )。
        如何对整个分布区域内的点（无数个）进行损失值的加权求和？
        用采样数据代替全部数据，用采样的个数代替加权（越靠近均值的取点数越多，与靠近边缘的取点数越少）。
        4.意想不到的问题
        
        看起来似乎已经很完美了，但实际上照着前面的思路它还会犯与AE差不多的问题，机器根本不跟你思路走，只要把方差搞的小小的，也可以满足需求嘛，这不就又变得跟AE似的了。
        显然这不是我们所希望看到的，最好是把分布搞的“矮矮的”、“胖胖的”，重叠越多越好。
        那怎么办那？解决方法还是在loss上下功夫，给loss下限制，让数据集所有样本对应的隐空间分布叠加起来越像高斯分布越好，根据数学所学的的知识不难知道，这样可以强迫每个组成分布变得“矮胖”。
        另一种解释的角度
        VAE的思路是模型重构，但这个重构的过程受到噪声的影响。但是这个噪声的强度（方差）也是通过神经网络获得的，因此模型为了能够更好的重构，会尽可能让噪声为0，即方差会趋于零。
        方差为零的话，也就没有随机性了，模型就退化成普通的AE了，噪声就不再起作用了。
        因此VAE还让所有的P（Z | X）都向标准正态分布看齐，这样就可以防止方差为0。
        假设所有的P（Z | X）都接近标准正态分布N（0,I），那么根据定义：
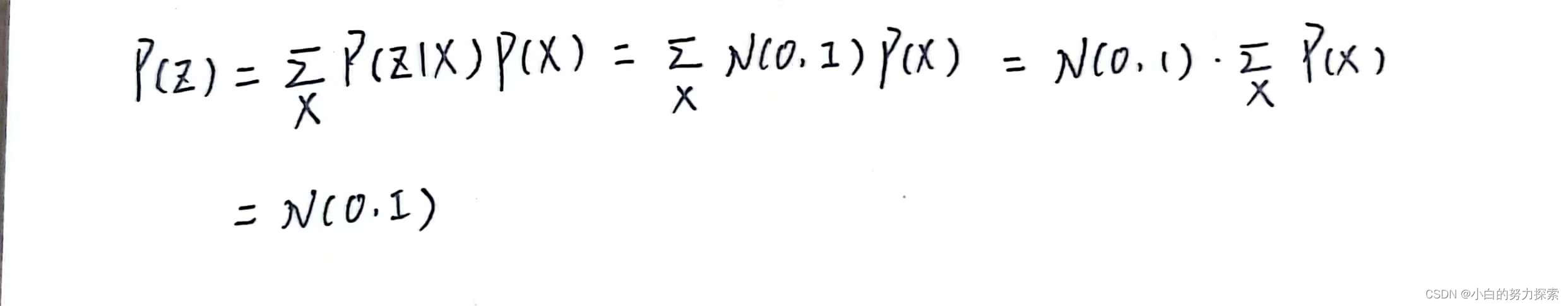
        因此P（Z）满足标准正态分布，符合了论文的先验假设，然后我们在生成数据的时候就可以在标准正态分布下采样了，这就保证了VAE有生成的能力。
        为什么是正态分布？对于P（Z | X）和P（Z）的分布为什么选择正态分布？均匀分布不可以吗？
        首先这是个实验问题，两种分布都试试嘛。其次直觉上讲确实是正态分布更靠谱，正态分布能在均值不变的情况下，改变方差
        5.现在的VAE能做到什么
        
        通过以上操作达到了什么境界
        隐空间有规律可循，长得像的数据会离的更近。
        隐空间随便取一个点，生成的东西多少都有点意义，这是因为除了分布的均值会被算loss，边缘部分也会被考虑。
        正是因为附近的点也会被抓包，所以相似含义的数据一定会离得相对较近，但又不会太近，因为中心区域被多次采样，所以势必会特色鲜明，不可能与别的类离得太近。
        正是这种相似数据离得近，但又不成簇，也不会离得太远，使得VAE有做分类器的潜质。
        code有规律，有含义，有区分，有过渡，完全可以用于生成。
        至于压缩编码，完全可以用均值当编码。
        方差是为了算loss，划定分布用的。
        6.VAE为什么好
        
        总之，就是VAE利用巧妙的结构和损失函数，对网络实现了约束，解决了AE的缺点，使AE的应用潜能真正能够实现。
        此外，VAE也可以应对GAN的三大缺点（训练不稳定，难以逆向，不提供密度估计）
        四.VAE的公式推导
        
        从上面的介绍不难发现，VAE的重点是对损失函数的构建，但先别急，先从建模z的分布开始下手。
        
        隐变量Z与X是紧密相关的，不妨设Z ~ P（Z | X）
        
        但数据集X的数据是有限的，因此P（Z | X）是未知的，只能基于现有的数据，通过编码器近似一个分布，Z ~ Q(Z | X)。
        
        我们希望它俩尽可能相似，因此引入KL散度来衡量相似度，进而优化问题就变成了最小化KL散度。
        
        因此优化问题就变成了对下式求最小化
        
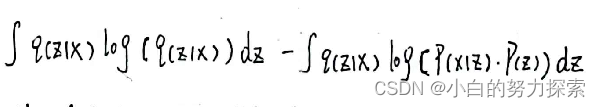
        做个正负变换，将优化问题转换为最大化下式问题。
        
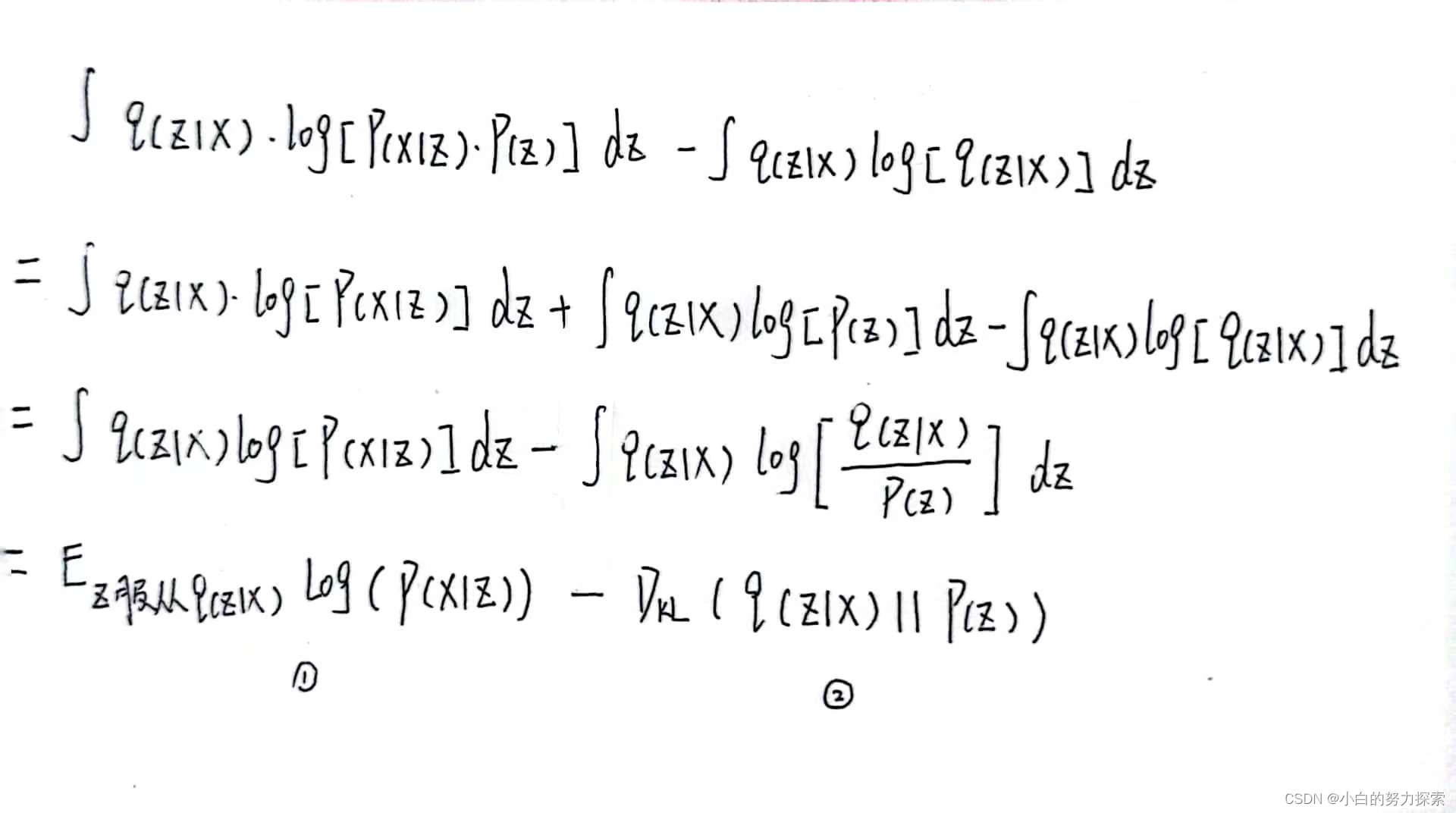
        第一项是不断的从样本集X确定的分布Z中采样一个z，希望z重建的输入x期望最大。
        因此P（ X | Z ）是解码器，记为P(X | Z ; θ)，可以理解第一项为是对解码器的束缚。
        而一般期望不好直接求，所以可以用其他的代替，比如说分类（离散）问题就用交叉熵，生成（连续）问题就用MSE。
        第二项是由X近似的Z的分布Q（Z | X）（一般符合高斯分布）与真实的Z的分布P（Z）的相似程度，与P（Z | X）一样P（Z）是未知的（论文中假设它是标准正态分布）。
        Q（Z | X）是编码器，记为Q(Z | X ;φ)，可以视第二项为对编码器的约束。
        对第二项的化简，如下图。
        综上所述，不难得到，当VAE用于数据（图像）生成时的损失函数为
        
        尽管我们通过公式推导出损失函数应该是上面的形式，但是有没有可能只这两部分中的一个也是可以的？答案是不行的，详见下图。
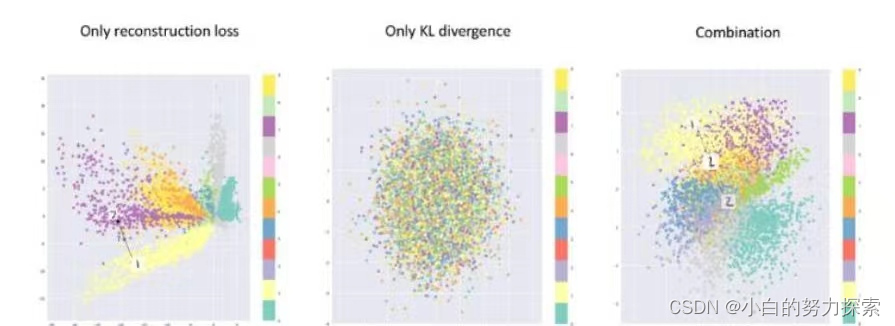
        由上图不难发现
        如果只用重构函数，就会得到和AE类似的结果，这正对应了我们3.4说的那种问题。
        如果只用KL散度的话，那么每个类别的数据对应的分布会更倾向于标准正态分布，彼此混叠，缺乏语义。
        只有两者兼顾，才能达到我们的设计预期。
        因此损失函数的两个部分缺一不可。
        总之，重构的过程是希望Z是没有噪声的，而KL损失是希望有高斯噪声的，两者对立。与GAN类似有一种对抗的意味在里面，通过对抗找到一个平衡，实现共同进化。
        五.重新参数技巧（reparameterization trick）
        
        P（ Z | X ）的分布是正态分布，每次在分布中随机采样一个点，然而“采样”操作是不能反向传播的，因此引入重新参数化技巧。
        重新参数化技巧的底层逻辑是：“采样操作”是不能求导的，但是“采样结果”是可以求导的。
        这样就把从N(μ,σ)里采样变成了从N（0，I）里采样，然后通过参数变换得到从N(μ,σ)里采样的结果。
        因为从N（0，I）里采样的过程，独立于网络之外，因此“采样操作”就不用参与到剃度下降的运算中了，取而代之的是将“采样结果”参与到计算中，这就使得整个模型可训练了。
        六.代码实现
        
        """ VAE网络架构与损失函数的实现 """ import torch from torch import nn import torch.nn.functional as F class VAE(nn.Module): def __init__(self): super(VAE, self).__init__() # 编码器所用的结构 self.fc1 = nn.Linear(784, 200) self.fc2_mu = nn.Linear(200, 10) # 用于生成高斯分布的均值 self.fc2_log_std = nn.Linear(200, 10) # 用于生成高斯分布的方差，且为方便计算默认方差是经过log函数处理的。 # 解码器所用的结构 self.fc3 = nn.Linear(10, 200) self.fc4 = nn.Linear(200, 784) def encoder(self, x): h1 = F.relu(self.fc1(x)) mu = self.fc2_mu(h1) # 生成均值 log_std = self.fc2_log_std(h1) # 生成经过log处理的方差 return mu, log_std def decoder(self, z): h3 = F.relu(self.fc3(z)) recon = torch.sigmoid(self.fc4(h3)) # 之所以用sigmoid是因为本例用到的图像默认像素值为0-1之间。 return recon def reparametrize(self, mu, log_std): std = torch.exp(log_std) # 因为生成的方差是经过log处理的，所以真正要用到方差的时候要再把它经过exp处理一下。 eps = torch.randn_like(std) # 在标准正态分布中采样 z = mu + eps * std # 获得抽取的z return z def forward(self, x): mu, log_std = self.encoder(x) z = self.reparametrize(mu, log_std) recon = self.decode(z) return recon, mu, log_std # 返回重构的图，均值，log后的方差 def loss_function(self, recon, x, mu, log_std) -> torch.Tensor: # 定义损失函数 ,注：-> torch.Tensor似乎没啥用，见test.py recon_loss = F.mse_loss(recon, x, reduction="sum") # use "mean" may have a bad effect on gradients kl_loss = -0.5 * (1 + 2*log_std - mu.pow(2) - torch.exp(2*log_std)) kl_loss = torch.sum(kl_loss) loss = recon_loss + kl_loss return loss
        
        """VAE简单应用举例""" import torch from torch import optim from torch.autograd import Variable from torch.utils.data import DataLoader from torchvision import transforms from torchvision.utils import save_image from torchvision.datasets import MNIST import os import datetime from vae import VAE if not os.path.exists('./vae_img'): os.mkdir('./vae_img') def to_img(x): x = x.clamp(0, 1) # torch.clamp(input,min,max) 把输入的张量加紧到指定区间内 x = x.view(x.size(0), 1, 28, 28) # batch，channel,w,h return x num_epochs = 100 batch_size = 128 img_transform = transforms.Compose([ transforms.ToTensor() # transforms.Normalize((0.5,0.5,0.5),(0.5,0.5,0.5)) ]) dataset = MNIST('./data', transform = img_transform, download=True) datalodader = DataLoader(dataset, batch_size=batch_size,shuffle=True) start_time = datetime.datetime.now() model = VAE() if torch.cuda.is_available(): print('cuda is ok!') model = model.to('cuda') else: print('cuda is no!') loss_function = VAE.loss_function optimizer = optim.Adam(model.parameters(),lr=1e-3) for epoch in range(num_epochs): model.train() train_loss = 0 for batch_idx, data in enumerate(datalodader): img, _ = data img = img.view(img.size(0), -1) # 把图像拉平 img = Variable(img) # tensor不能求导，variable能（其包含三个参数，data：存tensor数据，grad：保留data的梯度，grad_fn：指向function对象，用于反向传播的梯度计算）但我印象中好像tensor可以求梯度见13讲 img = (img.cuda() if torch.cuda.is_available() else img) optimizer.zero_grad() recon_batch, mu, log_std = model(img) loss =loss_function(recon_batch, img, mu, log_std) loss.backward() train_loss += loss.item() optimizer.step() if batch_idx % 100 == 0: end_time = datetime.datetime.now() print('Train Epoch: {} [{}/{}({:.0f}%] Loss:{:.6f} time:{:.2f}s'.format( epoch, batch_idx * len(img),len(datalodader.dataset), loss.item()/len(img), (end_time-start_time).seconds )) print('====> Epoch: {} Average loss: {:.4f}'.format( epoch, train_loss/len(datalodader.dataset) )) if epoch % 10 == 0: # 生成图像 if torch.cuda.is_available(): device = 'cuda' else: device = 'cpu' z = torch.randn(batch_size, 20).to(device) out = model.decoder(z).view(-1,1,28,28) save_image(out, '.vae_image/sample-{}.png'.format(epoch)) # 重构图像 save = to_img(recon_batch.cpu().data) save_image=(save, './vae_img/image_{}.png'.format(epoch)) torch.save(model.state_dict(),'./vae.pth')

微信扫一扫加客服

微信扫一扫加客服

点击启动AI问答