数据结构——图、查找

图

图的基本术语

1.端点和邻接点：

（i，j):顶点i和顶点j为端点，它们互为邻接点

2.顶点的度、入度和出度

无向图中，以顶点i为端点的边数称为该顶点的度

有向图中，以顶点i为终点的入边的数目，称为该顶点的入度，以顶点i为始点的出边的数目，称为该顶点的出度。i的度=入度+出度

3.完全图：

无向图中，每两个顶点之间都存在着一条百年，称为完全无向图，包含有n(n-1)/2条边

有向图中，每两个顶点之间都存在着方向相反的两条边，称为完全有向图，包含n(n-1)条边

边数最多时的图就是完全图

4.权和网：

图中的每一条边都可以附带一个对应的数值，这种与边相关的数值称为权，权表示一个顶点到另一个顶点的距离或花费的代价

边上带有权的图称为带权图，也称为网

图的存储结构＆基本运算算法

图的两种主要存储结构：

邻接矩阵；邻接表

邻接矩阵的主要特点：

一个图的邻接矩阵表示是唯一的，特别适合于稠密图的存储；存储空间是O(n2)

图的邻接矩阵存储类型定义：

 # define MAXV
 typedef struct
 {
     int no;//顶点编号
    InfoType info; //顶点其他信息
 }VertexType;
 typedef struct //图的定义
 {
     int edges[MAXV][MAXV]//邻接矩阵
         int n,e;//顶点数，边数
     VertexType vexs[MAVX];//存放顶点信息
 }MathGraph;

图的邻接表存储类型定义：

 typedef struct ANode
 {
     int adjvex;   //该边的终点编号
     struct ANode *nextarc; //指向下一条边的指针
     InfoType weight; //该边的权值等信息
 }ArcNode;
 typedef struct Vnode{
     Vertex data;  //顶点信息
     ArcNode *firstarc;  //指向第一条边
 }VNode;
 typedef struct{
     VNode adjlist[MAXV]; //邻接表
     int n ,e;   //图中顶点数n和边数e
 }AdjGraph;
 ​

图的遍历方法

深度优先遍历（DFS）

用栈或递归方法实现

从图中的某个初始点v出发，首先访问初始点v,然后选择一个与顶点v相邻且没被访问过的顶点w,以w为初始顶点，再从它出发进行深度优先遍历，直到所有顶点被访问。

 int visited[MAX]={0}//全局数组
 void DFS(AdjGraph * G,int v){
     ArcNode *p;
     visit[v]=1;
     print("%d",v);
     p=G->adjlist[v].firstarc;
     while(p!=NULL){
         if(visit[p->adjvex]==0)
             DFS(G,p->adjvex);
         p=p->nextarc;
     }
     
           }

树和二叉树

树

树的基本术语：

1.结点的度和树的度：

树中一个结点的子树的个数称为该结点的度。树中各结点的度的最大值称为树的度。

2.分支结点和叶结点：

度不为零的结点称为非终端结点，又叫分支结点。度为零的结点称为叶结点。

度为1的结点称为单分支结点，度为2的结点称为双分支结点。

3.孩子结点、双亲结点、兄弟结点：

在一棵树中，每个结点的后继，被称作该结点的孩子结点，相应的，该结点被称作孩子结点的双亲结点。具有同一双亲的孩子结点互为兄弟结点。

4.子孙结点和祖先结点：

在一棵树中，一个结点的所有子树中的结点称为该结点的子孙结点。从根结点到达一个结点的路径上经过的所有结点被称作该结点的祖先结点。

树的性质：

1.树中的结点数等于所有结点的度数之和加1

2.所有结点度数之和=n-1;所有结点度数之和=n1+2n2+...+mnm;n=n0+n1+..+nm

二叉树

定义：由一个根结点和两棵互不相交的称为左子树和右子树的二叉树组成。

两种特殊的二叉树：

1.满二叉树：所有分支结点都有双分结点，叶结点都集中在二叉树的最下层

2.完全二叉树：最多只有下面两层的结点的度数小于2；最下面一层的叶结点都依此排列在该层最左边的位置上

性质：

非空二叉树上叶结点数等于双分支结点数+1，即n0=n2+1

二叉树的遍历：

1.先序遍历：先访问根结点，再遍历左子树，再遍历右子树；先序序列的第一个结点是根结点

2.中序遍历：先遍历左子树，访问根结点，遍历右子树；中序序列的根结点左边是左子树的结点，右边是右子树的结点。

3.后序遍历：

先序遍历的递归算法：

 void PreOrder(BTNode *b){
     if(b!=NULL){
         print("%c",b->data);//访问根结点（此处的访问是指直接输出结点值
         PreOrder(b->lchild);//遍历左子树
         PreOrder(b->rchild);//遍历右子树
     }
 }

查找

定义

给定一个值K，在含有n个元素的表中找出关键字等于K的元素。若找到，表示查找成功，返回该元素的信息或该元素在表中的位置；若找不到，则查找失败，返回相关的指示信息

内查找和外查找

若整个查找过程都在内存中进行，则称之为内查找；反之，若查找过程中需要访问外存，则称之为外查找

查找方法的性能指标

查找运行时间主要花费在关键字比较上，通常把查找过程中执行的关键字平均比较个数作为衡量一个查找算法效率优劣的标准。

平均查找长度ASL:

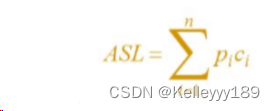
其中n是查找表中元素的个数,pi是查找第i个元素的概率，一般，认为每个元素的查找概率是相同的，即pi=1/n，ci是找到第i个元素所需进行的比较次数。

成功情况下的平均查找长度——ASL成功

不成功(失败)情况下的平均查找长度——ASL不成功

总的平均查找长度（ASL）可以通过下面的公式计算：

ASL=Ps⋅ASL成功+Pf⋅ASL失败

其中：

• Ps 是查找成功的概率。

• Pf是查找失败的概率。

• ASL成功 是查找成功的平均查找长度。

• ASL失败 是查找失败的平均查找长度。

  一般情况下，Ps +Pf=1，因为查找要么成功，要么失败。在这个公式中，你需要知道查找成功和查找失败的概率，然后分别计算对应情况下的平均查找长度。例如，如果所有元素被查找的概率相等，那么Ps=1/n（n是数据集中的元素个数），Pf=n-1/n。这样就可以计算得到总的平均查找长度。

  ASL是衡量查找算法性能好坏的重要指标。一个查找算法的ASL越大，其时间性能越差；反之，一个查找算法的ASL越小，其时间性能越好。

  

  

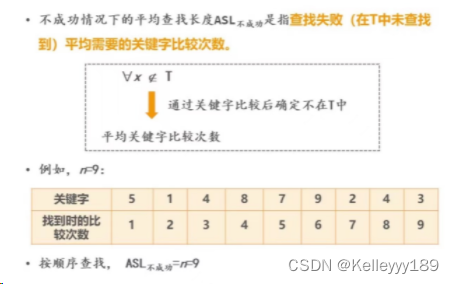
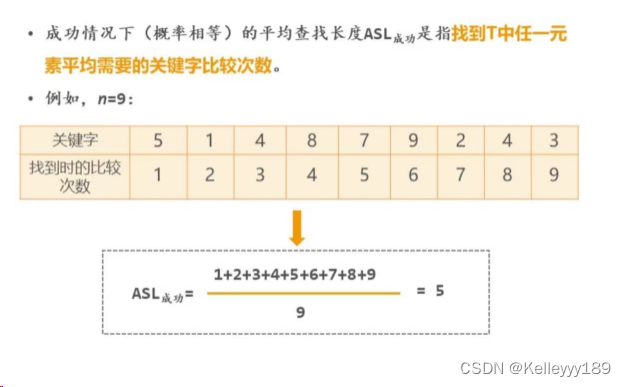
  线性表查找的主要方法

  顺序查找

  基本思路：从表的一端向另一端逐个将元素的关键字和给定值K比较，若相等，则查找成功，给出该元素在查找表中的位置；若整个查找表遍历结束后仍未找到关键字等于K的元素，则查找失败

  顺序查找算法：

   int SeqSearch(RecType R[],int n,KeyType k)
   {
       int i = 0;
       while(i=0)              //未找到返回0
           return 0;
       else
           return i+1;      //找到返回逻辑序号i+1
   }

  成功时的顺序查找的ASL为：ASL成功=\frac{1}{n}\quad× \frac{n*(n+1)}{2}\

  若K值不在表中，ASL不成功=n

  此顺序查找算法的平均时间复杂度为O(n)

  哨兵：在R的末尾加一个关键字为K的元素，称之为哨兵，增加哨兵后查找过程不再需要判断i是否超界限，从而提高查找速度

   int SeqSearch(RecType R[],int n,KeyType k)
       int i = 0;
       R[n].key=k;
       while(R[i].key!=k)
           i++;
       if(i==n)
           return 0;
       else
           return i+1;

  总结：顺序查找的优点是算法简单，且对表的存储结构无特别要求，缺点是查找效率低，因此当N值较大时不宜采用

  折半查找

  要求：所查找的线性表是有序表，即表中的元素按关键字有序排序，在下面的讨论中，假设有序表是递增有序的。

  基本思路：设R[low..high]是当前的查找区间，首先确定该区间的中点位置mid=[(low+high)/2],然后将待查找的K值与R[mid].key比较

  (1)若k=R[mid].key,则查找成功，并返回该元素的逻辑序号

  (2)若kR[mid].key,则新的查找区间是R[mid-1..high]

  折半查找算法：

   int BinSearch(RecType R[],int n,KeyType k)
   {
       int low=0, high=n-1, mid;
       while(lowk){  //继续在R[low..mid-1]中查
               high = mid-1;
           }
           else
               low=mid+1;     //继续在R[mid+1..high]中查
       }
       return 0;
   }

  时间复杂度：O(log 2n)

  树表的查找

  以二叉树或其他树作为查找表的组织形式，称为树表，树表主要采用链式存储结构，这类存储结构不仅适合于查找，也适合于插入和删除操作，属于动态查找表 。

  二叉排序树

  满足以下性质的二叉树

  1. 若它的左子树非空，则左子树上所有的结点值均小于根结点值

  2. 若它的右子树非空，则右子树上所有的结点值均大于根结点值

  3. 左右子树本身又各是一棵二叉排序树

     注：二叉排序树中没有相同关键字的结点

     

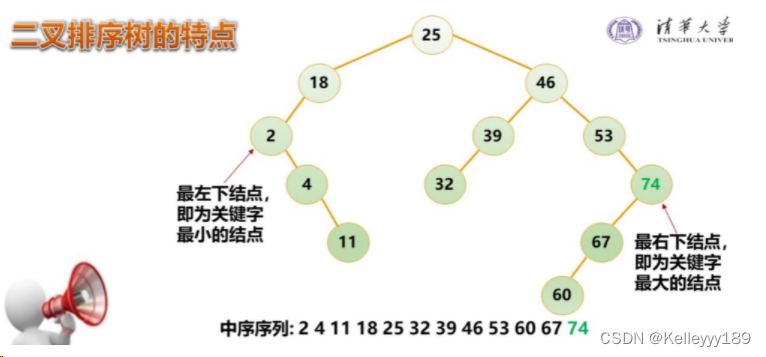
     特点：二叉排序树的中序序列是一个递增有序序列；根结点的最左下结点是关键字最小的结点；根节点的最右下结点时关键字最大的结点。

  二叉排序树的结点类型：

   typedef struct node{
       KeyType Key;//关键字项
       Info Type data;//其他数据域
       struct node *lchild,*rchild;  
   }BSTNode

  二叉排序树的插入和创建：

  在二叉排序树中插入一个关键字为k的新结点，保证插入后仍满足BST性质

  插入过程：

  1. 若二叉排序树bt为空，则创建一个KEY域为k的结点，将它作为根结点

  2. 否则将k与根结点的关键字比较，若kkey，则将k插入根结点的左子树中

  3. 若k > bt->key,将它插入右子树中

  4. 若k==bt->key,说明树中已有此关键字K,无须插入

     算法insertBS(bt,k):

      BSTNode* InsertBST(BSTNode*bt,KeyTyoe k){
          if(bt == NULL){//如果原树为空
              bt =(BSTNode*)malloc(sizeof(BSTNode)); //新建根结点bt
              bt ->key =k;
              bt ->lchild = b ->rchild =NULL;
          }
          else if(kkey)
              bt ->lchild =InsertBST(bt ->lchild,k);//插入到左子树中
          else if(k >bt->key)
              bt ->rchild=InsertBST(bt ->rchild,k);//插入到右子树中
          return bt;   //返回根结点
      }     // 先序遍历的思想

     创建二叉排序树：

     创建一棵二叉排序树是从一个空树开始的（bt=NULL);每插入一个关键字K,就调用一次insertBST(bt,k)算法将K插入到当前已生成的二叉排序树中。

      BSTNode *CreatBST(KeyType a[],int n){//返回树根指针
          BSTNode *bt=NULL;
          int i=0;
          while(ikey==k) //递归出口
              return bt;
          if(k key)
              return SearchBST(bt ->lchild,k);//在左子树中递归查找
          else 
              return SearchBST(bt ->rchild,k);//在右子树中递归查找
      }  //递归算法

      BSTNode *SearchBST(BSTNode *bt,KetType k){
          BSTNode *p=bt;
          while(p!=NULL){
              if(p->key ==k)
                  break;
              else if(kkey)
                  p=p->lchild;
              else if(k > p->key)
                  p=p->rchild;
          }
          return p;//返回查找结果
      }//非递归算法

     二叉排序树查找性能分析：

     查找成功的情况：

     从根结点开始，查找最后落在某个内部结点中，比较次数为该内部结点的层次；查找路径是二叉排序树的一部分

     在一棵二叉排序树上进行查找时的平均查找长度和其形态有关，含n个关键字的集合有n!个关键字序列，可以构造出 棵不同形态的二叉排序树。最坏情况：由有序序列创建的二叉排序树会蜕化成一棵高度为n的单支树，此时查找时间复杂度为O(n);最好情况：创建的二叉排序树形态比较均匀，此时查找时间复杂度为O(log2n)。所以一棵含n个结点的二叉排序树的查找算法的时间复杂度介于O(n)~O(log2n)之间

     二叉排序树的结点删除

     1.被删除的结点是叶子结点：直接删去该结点

     平衡二叉树

     定义：若一棵二叉树中每个结点的左右子树的高度至多相差1，则称此二叉树为平衡二叉树。

     平衡因子：该结点左子树的高度减去右子树的高度

     所有结点的平衡因子的绝对值小于或等于1，该二叉树成为平衡二叉树。

     平衡二叉树中插入关键字为k的新结点方式与二叉排序树相似，但插入后可能破坏平衡二叉树的平衡性，解决方法是调整。