简介
学习算法听起来很棒。但我们如何为神经网络设计这样的算法呢?假设我们有一个感知机网络,我们希望用它来学习解决某个问题。例如,网络的输入可能是扫描的手写数字图像的原始像素数据。我们希望网络学习权重和偏置,以便网络的输出能正确分类这个数字。要理解学习如何工作,假设我们在网络中对某个权重(或偏置)进行了小的改变。我们希望的是,权重的这个小改变只会导致网络输出中相应的小变化。正如我们马上要看到的,这个特性将使学习成为可能。示意性地,这里是我们想要的(显然这个网络太简单,无法做手写识别!):
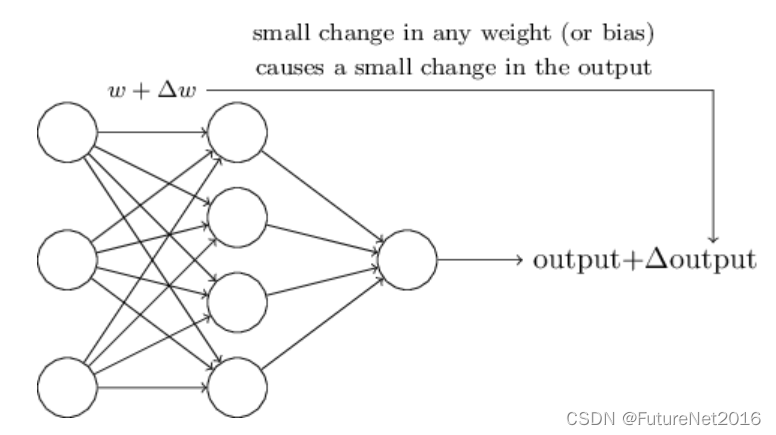
如果一个权重(或偏置)的小变化只导致输出的小变化是成立的,那么我们就可以利用这个事实来修改权重和偏置,使我们的网络行为更符合我们的期望。例如,假设网络错误地将一张图片分类为“8”,而它应该是“9”。我们可以找出如何微调权重和偏置,使网络更接近于将图片分类为“9”。然后我们重复这个过程,不断地修改权重和偏置,以产生越来越好的输出。网络就在学习。
问题在于,当我们的网络包含感知机时,情况并非如此。实际上,网络中任何单个感知机的权重或偏置的小变化有时会导致该感知机的输出完全翻转,例如从 0 变为 1。这种翻转可能会导致网络其余部分的行为以一些非常复杂的方式完全改变。因此,虽然现在你的“9”可能被正确分类了,但网络对所有其他图像的行为可能已经以某种难以控制的方式完全改变了。这使得很难看出如何逐渐修改权重和偏置,使网络更接近所需的行为。也许有一些巧妙的方法可以解决这个问题。但如何让一个感知机网络学习,并不是立即显而易见的。
我们可以通过引入一种新型的人工神经元——sigmoid神经元来克服这个问题。Sigmoid神经元与感知机相似,但已进行修改,使得它们的权重和偏置的小变化只会导致输出的小变化。这一关键事实将允许一个由sigmoid神经元构成的网络进行学习。
好的,让我描述一下sigmoid神经元。我们将以与描述感知机相同的方式来描绘sigmoid神经元:
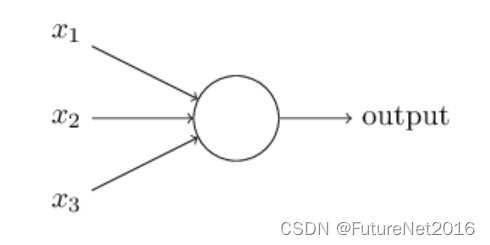
就像感知机一样,sigmoid神经元有输入x1,x2,… 但不同于感知机的输入仅限于0或1,这些输入还可以取0到1之间的任何值。例如,0.638…是一个有效的sigmoid神经元输入。与感知机相似,sigmoid神经元对每个输入都有一个权重w1,w2,…和一个总偏置b。但是,输出不是0或1。而是 σ(w⋅x+b) 其中σ被称为sigmoid函数。sigmoid函数定义为:

更明确地说,具有输入x1,x2,… 权重w1,w2,…和一个总偏置b的sigmoid神经元的输出是:
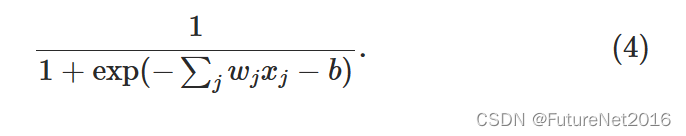
乍一看,sigmoid神经元与感知机似乎大相径庭。如果你还不熟悉sigmoid函数,其代数形式可能看起来既晦涩又令人生畏。实际上,感知机和sigmoid神经元之间有许多相似之处,而sigmoid函数的代数形式更多是一个技术细节,而不是理解的真正障碍。
要理解与感知机模型的相似性,假设 z≡w⋅x+b 为一个较大的正数。那么 e^−z ≈0 因此 σ(z)≈1。换句话说,当 z=w⋅x+b 很大且为正时,S型神经元的输出近似为 1,就像感知机的情况一样。另一方面,假设 z=w⋅x+b 非常负。那么 e^−z→∞,且 σ(z)≈0。因此,当 z=w⋅x+b 非常负时,S型神经元的行为也近似于感知机。只有当 w⋅x+b 处于适度大小时,与感知机模型存在较大偏差。
那么σ的代数形式呢?我们如何理解它?实际上,σ的确切形式并不那么重要——真正重要的是在绘图时函数的形状。下面是其形状:
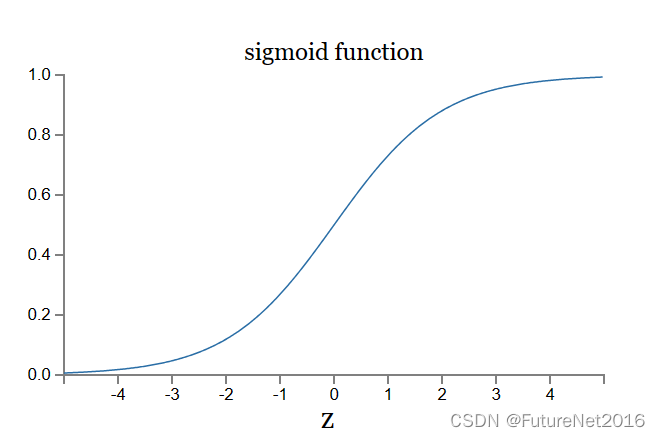
这个形状是阶跃函数的平滑版本:
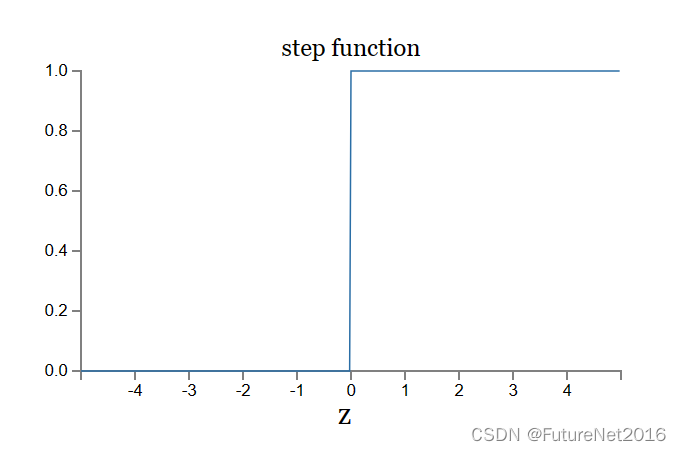
如果σ实际上是一个阶跃函数,那么S型神经元将是一个感知机,因为输出将取决于w⋅x+b是正还是负。
通过使用实际的σ函数,我们得到了一个平滑的感知机,正如前面已经暗示的那样。实际上,σ函数的平滑性是关键,而不是它的详细形式。σ的平滑性意味着权重中的小变化Δwj和偏差中的Δb将导致神经元输出的小变化Δoutput。实际上,微积分告诉我们Δoutput可以很好地近似为
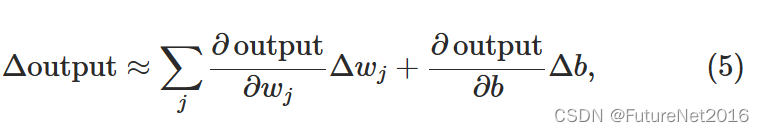
其中求和是针对所有权重wj,而∂output/∂wj和∂output/∂b分别表示输出相对于wj和b的偏导数。如果你对偏导数不太熟悉,不要惊慌!尽管上面的表达看起来很复杂,涉及到所有的偏导数,但实际上它表达的是非常简单的事情:Δoutput是权重和偏差的变化Δwj和Δb的线性函数。这种线性关系使得选择权重和偏差的小变化以实现输出的任意小变化变得很容易。因此,虽然sigmoid神经元在很大程度上具有与感知机相同的定性行为,但它们使得弄清楚改变权重和偏差将如何改变输出变得更加容易。
如果σ的形状真的很重要,而不是它的确切形式,那么为什么在方程(3)中使用了σ的特定形式呢?实际上,在本书的后面,我们偶尔会考虑输出为f(w⋅x+b)的神经元,其中f(⋅)是另一种激活函数。当我们使用不同的激活函数时,主要变化的是方程(5)中偏导数的特定值。事实证明,当我们稍后计算这些偏导数时,使用σ会简化代数运算,因为指数函数在微分时具有很好的性质。无论如何,σ在神经网络研究中是常用的,并且是本书中最常用的激活函数。
我们应该如何解释sigmoid神经元的输出?显然,感知机和sigmoid神经元之间的一个重大区别是,sigmoid神经元不仅输出0或1。它们的输出可以是0和1之间的任何实数,因此像0.173…和0.689…这样的值都是合法的输出。例如,如果我们希望使用输出值来表示输入到神经网络的图像的平均强度,这可能很有用。但有时它可能会成为一个麻烦。假设我们希望网络的输出指示“输入图像是一个9”或“输入图像不是一个9”。显然,如果输出是0或1,就像感知机一样,这将是最容易的。但在实践中,我们可以建立一种约定来处理这个问题,例如,决定将至少为0.5的任何输出解释为“9”,将小于0.5的任何输出解释为“不是9”。我会明确说明我们何时使用这样的约定,所以不应该造成任何混淆。








