提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档
目录
前言
一、机器学习
1.监督学习
（1）线性回归模型
（2）多元线性回归模型
（3）二元分类模型
（4）注意事项
（5）深度学习
（6）模型评估
（7）决策树
2.非监督学习
（1）聚类
（2）异常检测
（3）推荐系统
3.强化学习
二、RNN
三、RCNN
四、LSTM
五、Encoder-Decoder
六、Transformer
七、Bert
总结
参考资料
前言
从计算机之父Alan Turing 的 Computer Machinery and Intelligence 开始，将机器与思维联系到了一起，提出了著名的“图灵测试”，此后无数的科学家大牛们在这场“模仿游戏”中玩的不亦乐乎，将数学结合计算机形成了解决问题的系统，并且不断的深入，变得越来越复杂，从最初的的机器学习到现在动则几百亿参数的大模型；关于机器是否会拥有智能，硅基生物是否有一天会拥有自己的意识，当机器数据的规模不断增大，是否会量变引起质变，涌现出自己的思想，没有人可以给出一个肯定的回答，但是我们这个时代注定要见证许多的不平凡，过于先进的科技对于普通人来说就像魔法一样，希望通过自己不断地学习可以悟出魔法的奥秘。
一、机器学习
机器学习可以简单分为监督学习、非监督学习与强化学习。
监督学习是给出算法实例和答案，对输出进行预测或者分类，相对应用的比较多；
非监督学习是根据数据自己进行学习，例如给标签的数量自己进行分组集群（聚类/异常检测/降维）；
强化学习是根据环境的反馈进行强化学习。
1.监督学习
在监督学习中主要分为线性回归模型和分类模型
（1）线性回归模型
最简单的线性回归模型，就是给出数据，找到一条最合适的线（函数）来对其进行拟合，之后可以进行预测。线性回归模型和分类的区别之一就是分类的输出一般是有限的，而线性回归模型的输出基本是无限的。
所以我们只要给定训练数据xi和yi，假设函数为f，预测输出为y-hat
其中f就是要训练的模型，简单的可以是一元一次方程，复杂的可以有几百个参数。
那么问题就来了，我们该如何去找到这个 f 呢？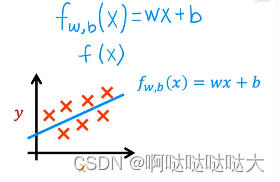
换句话说，要找到 f，就是要找到函数中的参数，也就是w和b，所以我们的目标转移到了找w,b的问题上。
在最开始我们先随便选择参数，构建一个预测函数，之后不断的调整使它更贴合训练集，所以我们的目标又转移到了如何去调整参数之上。
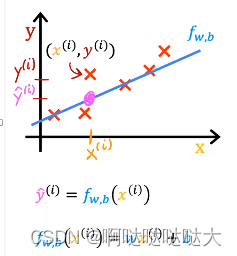我们现在的预测模型代入xi可以得到预测值，也可以看到它与真实值的差距，利用这个特点，我们就可以通过反向传播去训练这个参数，让预测值与真实值的差距越来越小，而反向传播的关键之一就是损失函数。
不要忘记我们的目的是去找w,b，而损失函数就是一个重点。
可以看到损失函数占大头的就是对所有训练集的预测值减去真实值的平方求和，之后除以2倍的训练集数量，只要知道他和那个“差值”是正相关的就足够，差越大，损失函数越大。如果我们暂时去除b这个参数，对w进行随机取值，得到的损失函数是这样的（如果加上b则变成3维图像）：
J对于w的函数图像
J对于w,b的函数图像
可以看到是存在w,b使得损失函数最小的，我们的目的是为了找到这个最合适的w,b，也就是为了减小这个损失函数、减小差值，于是又引出了梯度下降的概念。
梯度下降的目的就是为了找到这个最合适的w,b,也就是损失函数中的最小值所对应的参数。
在一开始我们随机给出了w,b,带入到损失函数之中，可以求出这个位置的偏导数，用现在的w减去学习率α与偏导的乘积，可以找到下一个更合适的位置；因为偏导为负数则为“下坡路”，减去负数得正前进继续下降找更小，反之上坡后退找更小，最终找到那个最低点。其中的学习率α也是线性回归模型中的超参数之一，是需要我们自己去设定的。在此也补充一下有关机器学习的相关概念,有助于对于以后内容的理解。
概念解释：
学习率α：机器学习的超参数之一，为了控制找最优w,b的步长，太大了容易爆炸，太小了找的太慢（也有可能找到了局部最优解就跳不出去了），建议是0.01~0.001刚开始可以用，在一定的epoch之后减缓，如果是迁移学习微调的话建议=0，>0是线性的
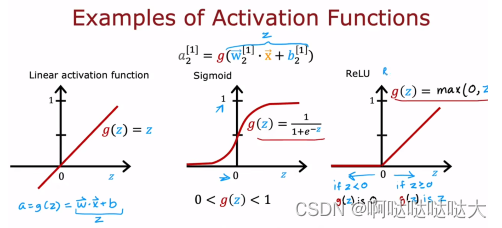
如何去选择隐藏层的激活函数，大部分都是ReLU，注意不能直接用线性回归模型，因为那样的话人工神经网络就是一个大型的线性回归模型就鸡肋了。
选择输出层的激活函数：输出层函数有所讲究，主要看需要的输出类型是什么样的，对应的激活函数的特点。二元分类用sigmoid，回归y分为正负用线性，y大于0用relu
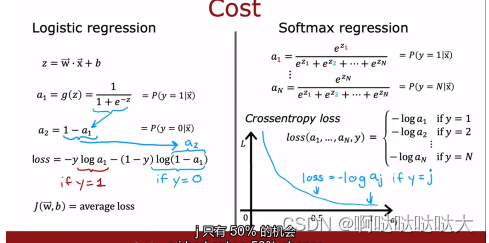
多分类模型：在之前提到了二分类模型，那么如果有多个输出的话，即多分类，应该如何进行？其实就采用了softmax多分类模型，简单来说是对输出又做了一个求比重的运算，从而得到多输出。
通过计算最后得到的输出ax就是对应x的概率
加入softmax之后损失函数也有所改变，变为对每个输出单独求损失函数
之后的流程也是大同小异，通过正向传播和反向传播更新参数，最终得到训练好的模型，如下：
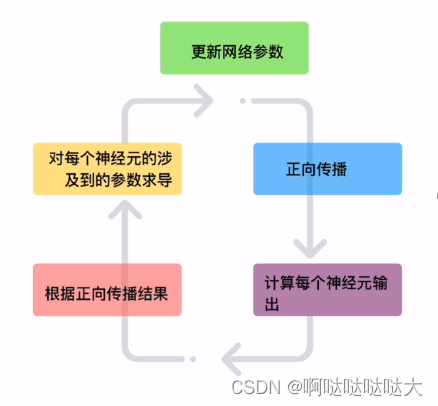
值得一提的事还有其他的算法可以取代梯度下降的算法，比如Adam算法等，很多比梯度下降好用
卷积神经网络（CNN）：卷积神经网络即CNN，Convolutional Neural Networks，就是在人工神经网络NN的基础之上，对输入层做改变，使每个神经元看一部分的输入，从而减小运算量。C代表的卷积，是对输入的一种处理，用来处理图像特征，卷积层拥有多个卷积核，每个卷积核都有自己的特征，之后对图像进行卷积处理，几个内核就会扫出来几张图。
提取出的特征图中矩阵的维数=[（input的维数-卷积核的维数+2*zero-padding）/stride]+1
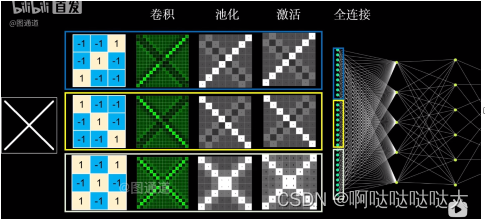
然后进行池化，就相当于压缩降维，每一块之中取最大值或者平均值来减小冗余，这也是下采样中的一种，拥有平移不变性。
卷积层的特征进行合并或者取样输入全连接层
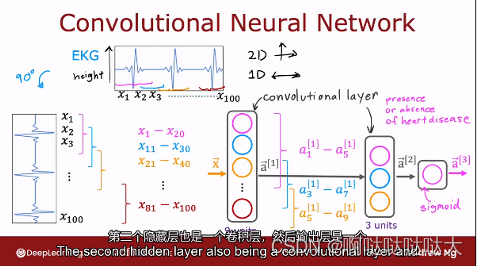
最后的效果如下：
（6）模型评估
当我们构建出一个又一个的模型之后，如何知道我们的模型是好是坏，以及如何进行修改，就涉及到了许多新的有关模型评估的概念。
首先是增加了交叉测试集Cross validation（cv or val)，简单来说就是对于你的训练集来说，如果有许多高阶多项式的话你的J train可能效果很好，但是J test很差，所以又增加了中间的一个缓冲地带交叉测试集：
这样的话当你在训练集上训练了十个模型都差不多的时候，可以选择在交叉验证集上效果最好的来应用到测试集上。
偏差方差：偏差bias—在测试集上的差；方差variance—在交叉测试集上的差
高偏差说明没训练好欠拟合，高方差低偏差说明过拟合，最好的结果是低偏差低方差
之前我们介绍α的概念之中提到了如何选择α，但是提到兰姆达的时候却没有提，因为要先有交叉验证集才能选择它。通过不断的尝试
选择在cv上最合适的作为最终选项
选择的时候也可以构建出对应的偏差和方差，得到最合适的点对应的兰姆达。专门看偏差和方差的函数称为学习曲线。
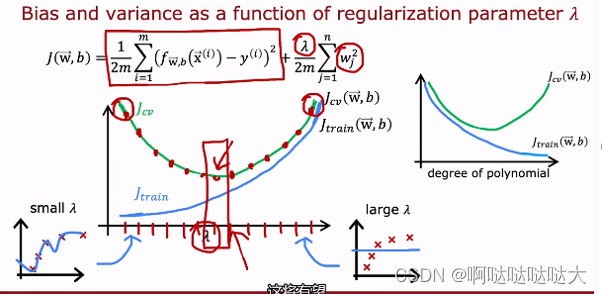
高偏差的话有可能是模型问题，看看增加数据，或者模型太简单，用更复杂的函数；
高方差的话考虑过拟合了，可以增加训练集的数量
通过观察偏差和方差可以有助于我们训练自己的模型，其它的方法还有数据增强，迁移学习等技巧，迁移学习在目前应用比较普遍，把已经训练好的模型应用于自己的数据之中，一般有两种选择，一是只再训练输出层；二是训练所有的参数
精确率和召回率：
精确率：预测1中有多少是正确的，预测正确率
召回率：真实的1中被预测中了多少
F1score用来算召回率和精确率的得分，进而评估模型。
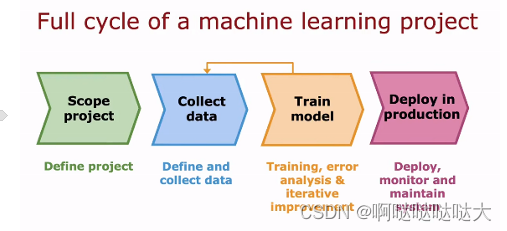
最后是深度学习的完整训练周期：
（7）决策树
决策树没好好学，只能简单介绍一下大概：
由根节点 决策节点 叶子节点构成
主要的问题是怎么去分特征最好？这个靠的是纯度
其次是分到什么程度？分到都是100%或者到最深的了
运用到了香农的信息论，H（p）熵
熵的图像如上所示，在p=0.5的时候最大为1
然后是选择分的节点
每个特征分完都有熵的大小和纯度，先求总的熵，再减去权重乘每部分的熵，得出的值越大说明减小的熵越多，就选这个点来分
有关决策树的内容如下：
或者使用one-hot编码：
每个特征是或者不是填入0/1，最后给出是或者不是0/1，形成一个表格，然后直接进行分类训练
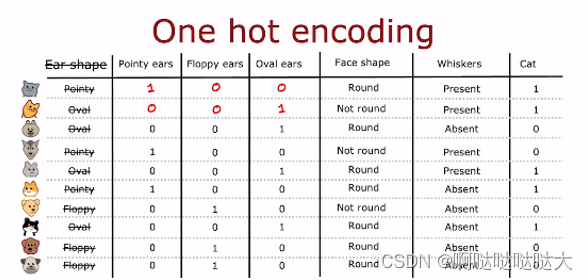
算出来每一个weights 。
多个决策树：随机森林
有关决策树和神经网络的对比，目前应用的更多的还是神经网络，但是决策树相对于神经网络最大的优势就是可解释性，这也是神经网络被诟病的原因之一。
2.非监督学习
非监督学习主要分为聚类、异常检测和推荐系统。
（1）聚类
聚类的方法有很多：
在这我们主要学习一下经典的K-means算法来找集群中心。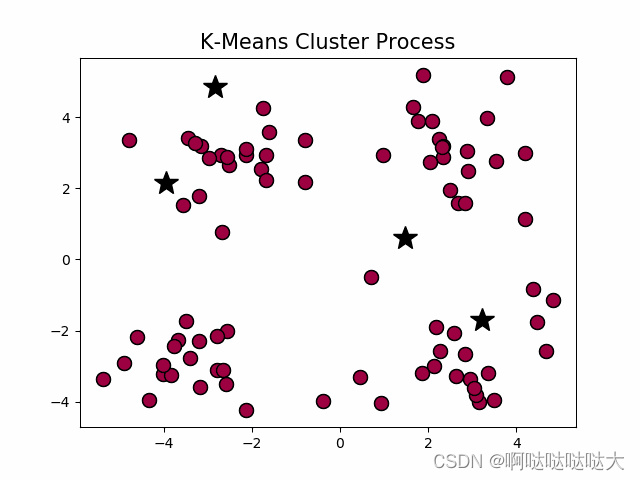
首先随机猜测中心在哪里，然后根据中心划分，之后再重新算这些数据的中心，以此反复找到最合适的中心点。
其中聚类也有损失函数，也是要找到损失函数的最小值。
聚类中关于K的数量的选择采用“肘法”
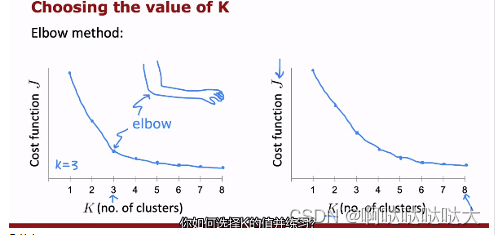
（2）异常检测
可以通过密度算法来找异常，也可以通过高斯分布来找异常，或者通过选择特征和加数值最后变成高斯分布来找异常。
步骤如下：
1、选取参与概率计算的特征值，必要时进行处理。
2、对于每个特征值，计算μ、δ，进而计算出每个特征值的概率公式pj(x)。
3、将所有参与计算的特征值的概率公式相乘，得到总的概率公式p(x)。注意，这里有个前提，是这些特征互相之间不想关，即互相独立。这种计算方式，称为极大似然估计（maximum likelihood estimation），也是概率论中的一种计算概率的方式。
4、对于一个给定的样本x，计算p(x)，如果p(x)
