🍿本文主题:动态规划 01背包 背包问题 C/C++ 算法
🎈更多算法:基础回溯算法 基础动态规划
💕我的主页:蓝色学者的主页
文章目录
- 一、前言
- 二、概念
- ✔️动态规划概念
- ✔️01背包的概念
- 三、问题描述与讲解
- 🎺题目描述
- ✔️Dp数组
- ✔️递推关系
- ✔️dp数组如何初始化
- ✔️打印dp数组
- 四、状态压缩-滚动数组
- 五、参考代码
- 六、结语
一、前言
很开心又和大家见面了,上次我们学习了基础算法——动态规划,那今天我们来一起学习一下的动态规划的进阶部分,通过一道很经典的动态规划题目,帮助大家掌握经典的01背包问题,之后我还会留下本节课的作业,感兴趣的话一起来看看吧~
二、概念
✔️动态规划概念
还记得我们上次文章讲解动态规划最重要的两个概念吗?
概念一:状态转移
概念二:Dp数组
如果你记不太清这两个概念,可以先去看我前面讲的基础动态规划,看完之后,再来尝试进阶动态规划会好很多~点我看基础动态规划
✔️01背包的概念
01背包问题简单来说就是,有i个物品,每个物品只有一个且有自己的价值value,把他们放到容量为j的背包里,问最大价值是多少?
这样解释后,我们就知道为什么叫背包问题了,可是还有一点不明确,为什么要叫01背包呢?
其实01只表示两个状态,选与不选,因为每种物品只有一件,我们只有这两种选择
三、问题描述与讲解
🎺题目描述
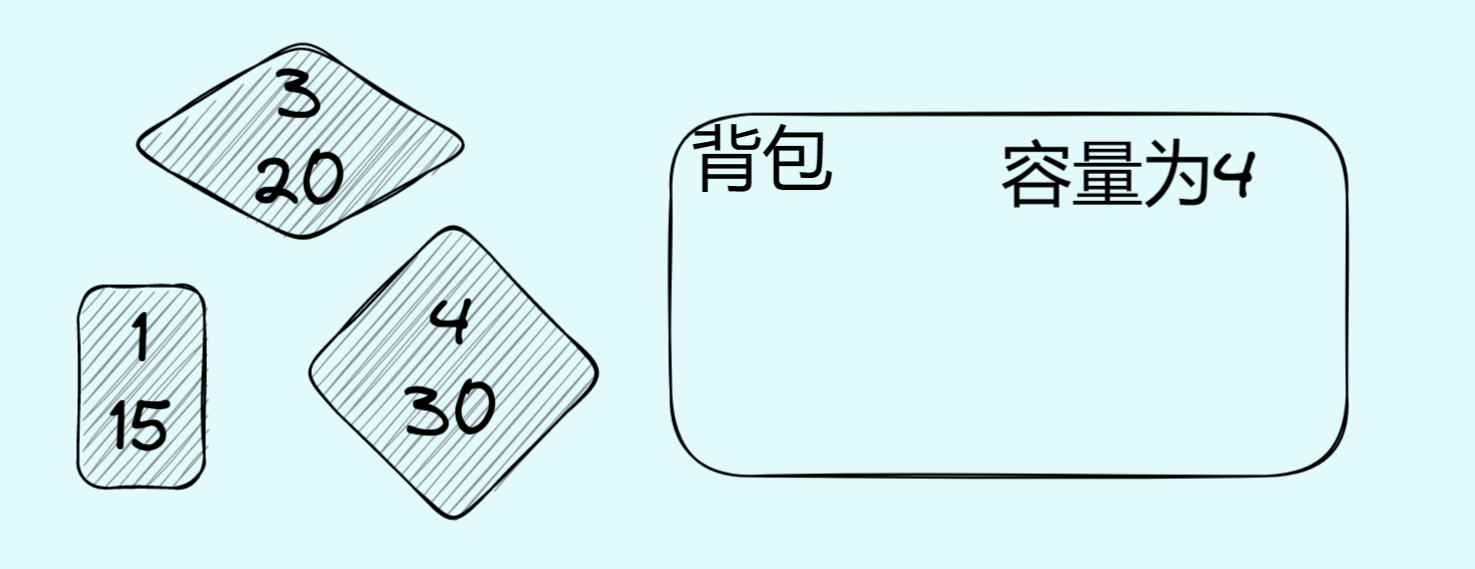
有三块石头,重量分别为{1,3,4};价值分别为{15,20,39};背包容量为4
问:怎么装才能让背包价值最高?
✔️Dp数组
题目问我们最大价值是多少,因此我们Dp数组表示的就是最大价值,我们要思考这个值是怎么来的?
那最终价值都跟什么有关呢?无非就是物品和背包容量!这里大家可能会很懵,我举个例子
- 假设石头只有第0个,那么最大价值是dp[0][j] 表示将第0个~第0个物品放到容量为j的背包里所产生的最大价值
- 假设石头有第0个,第1个,那么最大价值是dp[1][j]表示将第0个~第1个物品放到容量为j的背包里所产生的最大价值
大家这样就理解了吧,虽然我们可以使用dp[j]直接去表示容量为j的最大价值(之后将状态压缩的时候会讲解如何压缩为一维数组)但这里我们用二维数组来表示
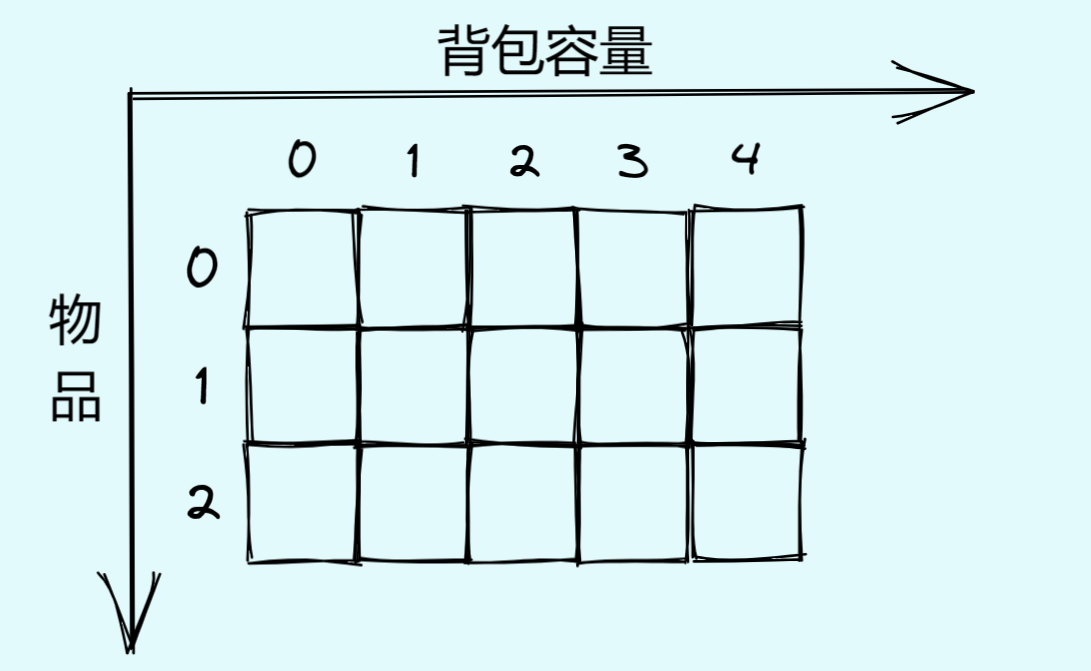
- dp数组的含义 dp[i][j] #表示将第0个~第i个物品放到容量为j的背包中所产生的最大价值!
✔️递推关系
当我们想不清楚递推关系的时候,不妨举个例子试着推导一下:如图
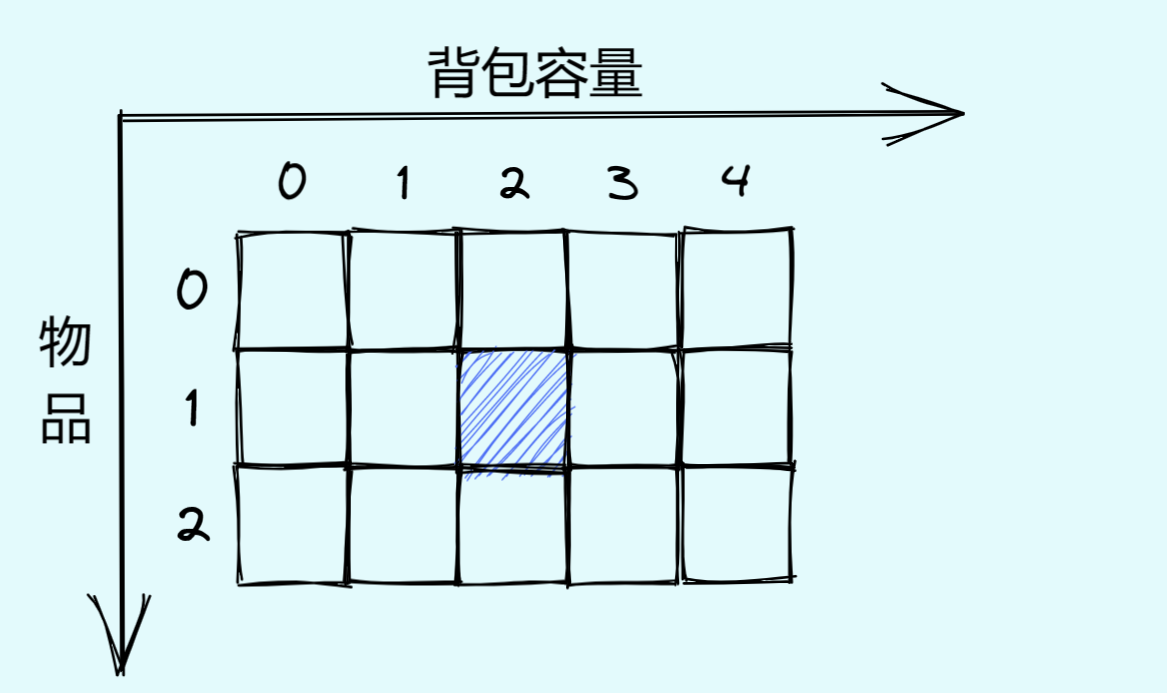
要求蓝色坐标位置的最大价值,我们来试着推导一下dp[1][2] ,就是让我们求有两个石块、背包容量为2的情况下的最大价值!
- 若不放物品1 ,那不久变成了只放物品0容量为2的背包的最大价值
- 若存放物品1 ,要事先预留下物品1的重量,结果就是除去物品1的重量后放前面物品产生的最大价值 + 物品1的价值
总结下来就是在这两种情况下选最大值,因此递推公式为:
希望大家能仔细感悟上面两种情况,这是01背包和动态规划的精髓!dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]] + value[i]); ✔️dp数组如何初始化
当背包容量为0的时候,我们取不了任何元素,因此也就没有最大价值~我们初始化为0
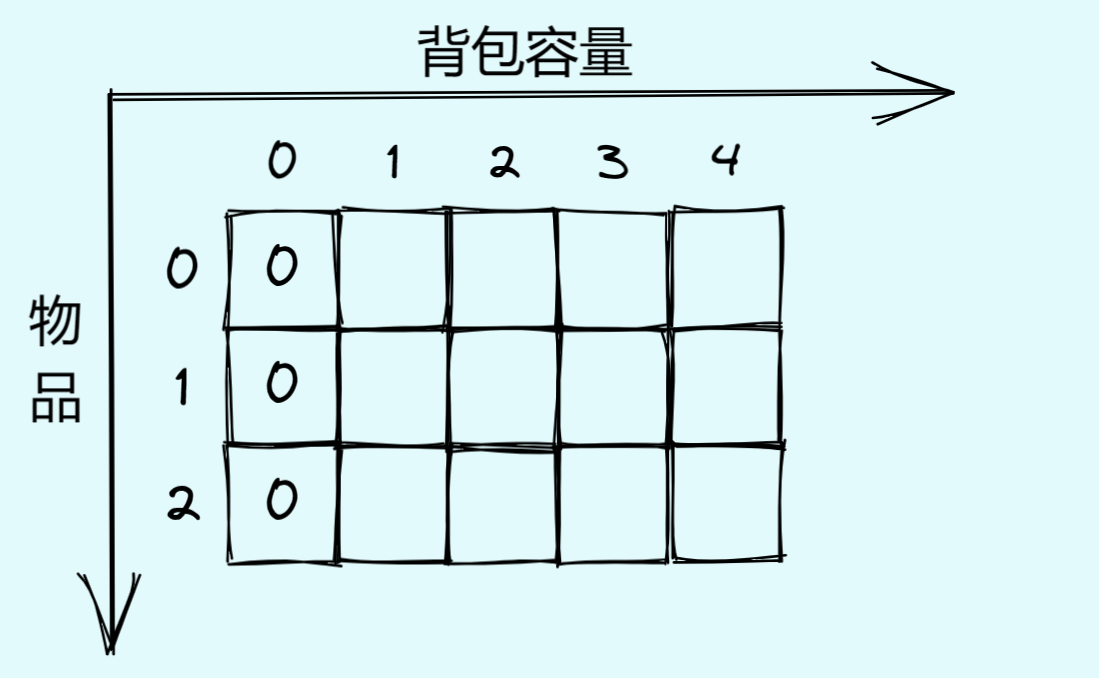
- 第一行我们也需要初始化,为什么?观察我们的递推公式:
dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]] + value[i]); 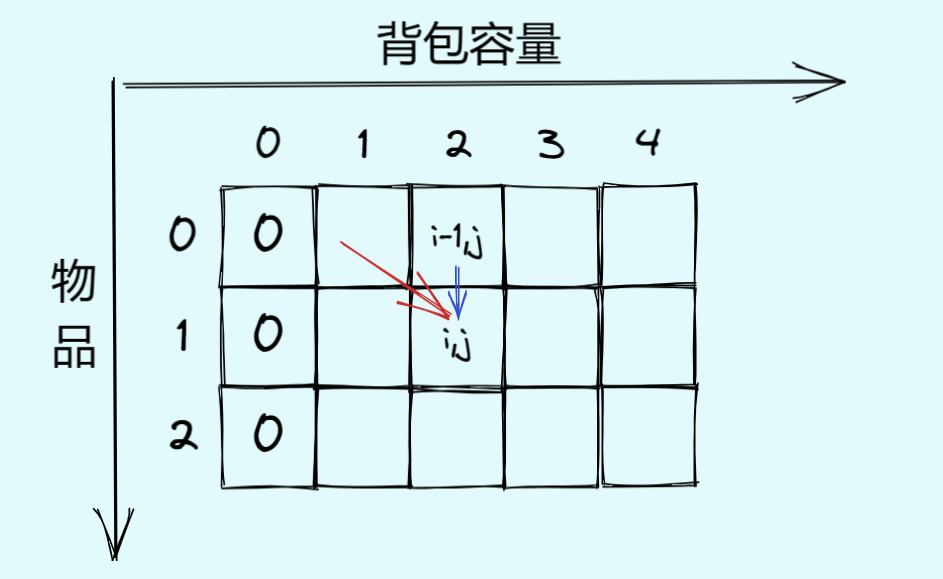
如图,dp[i][j] 的状态需要左上角的两个元素推导得出,但注意,红色箭头指的是左边某个元素,而不是正左上角!!
- 怎么初始化?
我们先看第一行的含义是什么,即只把第0个物品放到容量为0,1,2,3…的背包中产生的最大价值
这里并不是一股脑地把第一行全都赋值为第0个物品的价值,而是判断背包容量能不能装得下第0个物品,装得下才赋值为第0个物品的价值
复制完后如图:
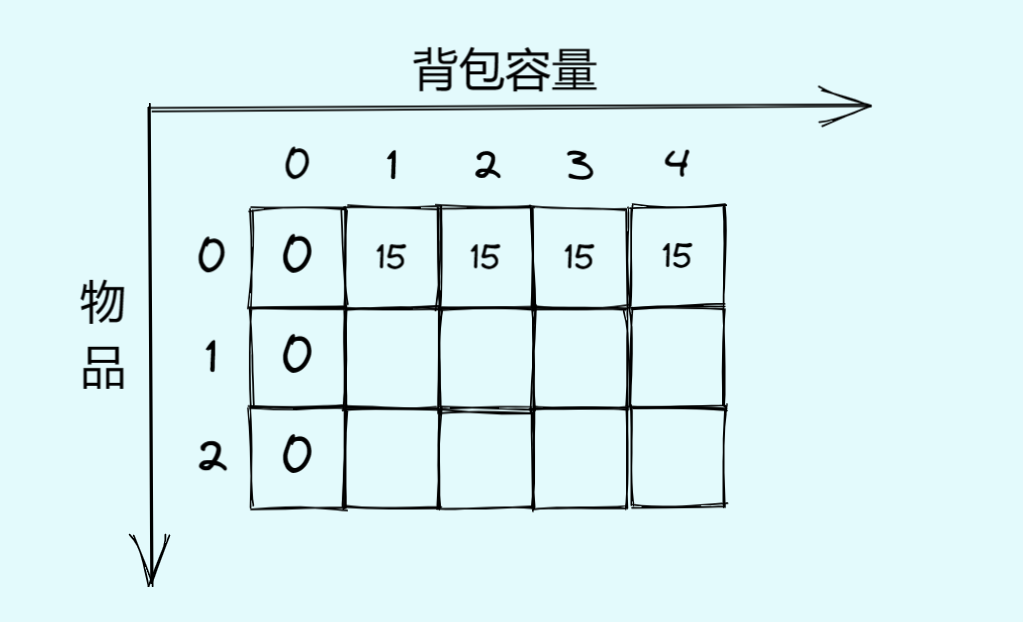
- 那其他元素的初始化呢?
其他元素由于是由其他元素推导得出,理论上可以是任何值,但不要忘了,我们在第一行元素初始化的时候,只对能装下物品0的元素赋值了,那装不下的背包应该赋值为多少?
当然是0!不然就会影响其他步骤判断!所以我们干脆就在一开始就初始化所有元素为0!
✔️打印dp数组
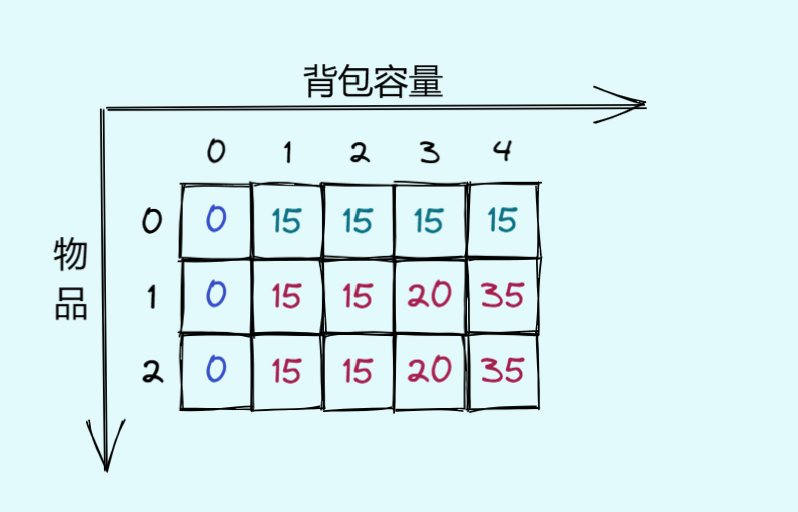
四、状态压缩-滚动数组
其实细心的同学已经发现了,我们递推关系中,指明第二行的元素全是由上两行元素推导得来,因此我们可以只创建一个一维数组,来简化代码,这又被称为滚动数组,实际上就是数据在不断被覆盖
实现这种代码比二维数组方式更为简单,大家可以去尝试一下,下次动态规划讲解,我们再重点讲解降维的思路
有两点需要注意:
一、必须先遍历物品,再遍历背包,因为我们是横向覆盖!不是纵向覆盖!
二、必须从右边向左边遍历,如果从左边向右边就会覆盖数据!因此我们是由左上角和正上方的数据推导而来!!
五、参考代码
#define _CRT_SECURE_NO_WARNINGS 1 #define MAX(a,b) ((a)>(b)?(a):(b)) #define row 3 #define BAGSIZE 4 #include #include #include int main() { int weight[] = { 1,3,4 }; int price[] = { 15,20,30 }; int Dp[row][BAGSIZE+1] = { 0 }; for (int i = 1; i = weight[0]) Dp[0][i] = price[0]; } for (int i = 1; i = 0) { Dp[i][j] = MAX(Dp[i - 1][j], Dp[i - 1][j - weight[i]] + price[i]); } else { Dp[i][j] = Dp[i-1][j]; } } } for (int i = 0;i for (int j = 0;j printf("%d ", Dp[i][j]); } printf("\n"); } }
- 那其他元素的初始化呢?
- 怎么初始化?
- 第一行我们也需要初始化,为什么?观察我们的递推公式:
- dp数组的含义 dp[i][j] #表示将第0个~第i个物品放到容量为j的背包中所产生的最大价值!